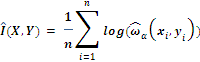Specification

The Financial Analysis library provides measures of statistical relation between series data based on linear Pearson’s product-moment correlation coefficient.

Pearson's Correlation Coefficient between two n-points data series

X = (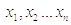 ) and Y = ()

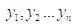is defined as

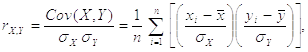
and lagged correlation:

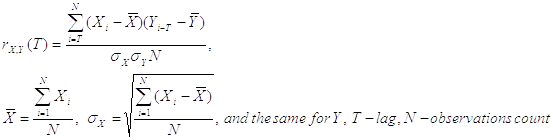
where:

 are average values over the series,

are standard deviations over the series,

 is covariation between X and Y.

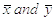
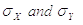
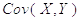
Correlation Coefficient is ranged from -1 to 1 and measures the extent to which values of two variables change "proportionally" each to other, i.e. as one variable increases, how much another variable tends to increase or decrease. The value of 1 represents a perfect positive correlation when both variables fluctuate around their means coherently, the value of -1 indicates exactly opposite tendency and the value of 0 represents a lack of correlation, i.e. linear statistical independency.

Although Correlation Coefficient is sensitive only to a linear relationship between two variables, it can also point out a nonlinear relationship between the variables.

The same formula applied to one variable X and describing the correlation between values of the variable at different time points (i.e. the correlation of the variable against a time-shifted version of itself) is called Autocorrelation Coefficient or Cross-Correlation Coefficient:

 

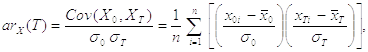
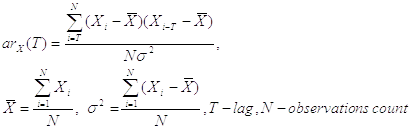
where:

T is time lag,

 are average values over the original and the lagged time series,

are standard deviations over the original and the lagged time series,

 is covariation between the series.

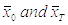
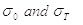
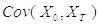
The Correlation and Autocorrelation Coefficients are commonly used for checking randomness in data series, to visualize correlations often Correlogram and Autocorellogram are used, that are spectrum-like plots of correlation coefficients at varying time lags.

One more available correlator is Mutual Information. In contrast to Pearson’s correlation, Shannon’s Mutual Information coefficient covers all kinds of statistical dependencies including nonlinear ones. Mutual Information of two random variables equals zero if and only if they are completely statistical independent.

Mutual information of two continuous random variables X, Y can be defined as:

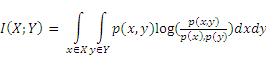
As the calculation of continuous MI by definition on limited statistical data set is impossible due to necessity of knowing exact probability distribution functions, we have to use approximations. The approximation of mutual information between two data series is calculated using Least Squares Mutual Information method. This indicator receives two values and allows to approximate mutual information between two user specified series, for instance Apple inc. and Microsoft corp. stock prices.

The density ratio function:

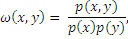
Where p(x, y), p(x), p(y) are the probability density functions. We apply the following model to the density ratio:

,

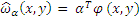
Where 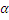 is a vector of parameters to be learnt from samples, and 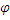 is a vector of basis functions.

Gaussian kernel:

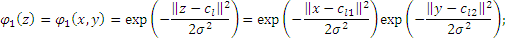
Gaussian kernel with Kronecker delta for second series (which intends to be discrete in this case). Note: if both series are discrete, following approximation doesn’t make any sense, cause there are much simpler, fast and accurate approximations.

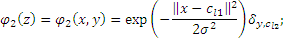
Where centers 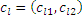 –selected randomly from samples, 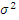– variance selected by Cross Validation procedure, and Kronecker Delta:

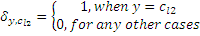
To determine 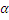 we use linear least squares optimization in order to find a minimum of the following functional with respects to the statistical data sets:

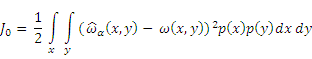
Given a density ratio estimation MI can be simply estimated by the following formula (over assumption that probability of al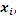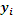l ( ) pair values are close to be equal: