AVL Tree

The AVL Tree is data-comparative search tree that relies on a comparison between the target search key and the key contained at each node along the search path to organize data objects to each other.

More specifically, an AVL tree is a Binary Search Tree (BST) with the additional balancing requirement.

As a Binary Search Tree, it contains a root node along with left and right binary search sub-trees of nodes such that (see Example):

• All the nodes in the left sub-tree contain keys (numerically, alphabetically or in other sense) less than or equal to the key of the root node;

• All the nodes in the right sub-tree contain keys greater than or equal to the key of the root node.

The AVL Tree was developed to overcome high imbalance in a BST and achieve a worst-case performance of O(log₂n) for the search, retrieve, insert and delete operations. AVL Tree is balanced with respect to the heights of its sub-trees, meaning height to be the length of the path from the root to the deepest leaf node in the tree.

Each node X of the AVL tree is assigned with the Balance Factor value:

Balance Factor of X = Height of right sub-tree of X - Height of left sub-tree of X.

If Balance Factor is 1, 0, or −1 then the node is considered balanced; otherwise the AVL tree is said unbalanced at the node X and this node is called the pivot node. Balancing is performed around pivot nodes using rotation techniques.

The balance of an AVL tree is checked and restored after each insertion and deletion of nodes.

Example

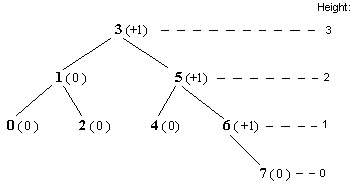
The following figure shows how seven (bold) keys can be organized using AVL Tree, numbers in round brackets are nodes' balance factors:

The AVL Tree is implemented by the AvlTreeTKey, TValue class designed to organize user-specific data type with user-specific key type.

The constructor AvlTreeTKey, TValue(Int32) creates new AVL tree. Use the constructor AvlTreeTKey, TValue(Int32) to create AVL tree with required number of preallocated elements.

To search and navigate over the data, the class provides special mechanism defined inside it and presented by the AvlTreeTKey, TValueAvlTreeIterator class.

For usability reason, the class presents AVL Tree as an array of tree nodes ordered by the keys ascendingly. AVL tree node is represented by the structure AvlTreeTKey, TValueEntry with a set of fields.

An instance of the AvlTreeTKey, TValueAvlTreeIterator is associated with this array or its part depending on search condition. This array is also supplied with commands (class methods) to navigate over the nodes; at each position the iterator can provide essential information about the corresponding tree node via the following class properties:

To create a new tree node use the following constructor:

AvlTreeTKey, TValueEntry(TKey, TValue, Int32, Int32, Int32, Int32, Int32)

Use the constructor AvlTreeTKey, TValueAvlTreeIterator(AvlTreeTKey, TValueEntry, Int32, Int32) to create an instance of the iterator.

Caution
Key type must implement the SystemIComparable interface.

AvlTreeTKey, TValueAvlTreeIterator provides positional navigation over the ordered array of nodes with its methods:

The AvlTreeTKey, TValue class provides the following methods:

The class provides properties: