Signal Processing |
Signal processing section is devoted to discrete Fourier transform of the input signal.
The discrete Fourier transform (DFT) is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function. An input function must be discrete, with its non-zero values of limited (finite) duration. Such inputs are often created by sampling a continuous function, like a person's voice.
The input to the DFT is a finite sequence of real or complex numbers, making the DFT ideal for processing information stored in computers.
In particular, the DFT is widely employed in signal processing and related fields to analyze the frequencies contained in a sampled signal, to solve partial differential equations, and to perform other operations such as convolutions or multiplying large integers. A key enabling factor for these applications is the fact that the DFT can be computed efficiently in practice using a fast Fourier transform (FFT) algorithm.
This topic contains the following sections:
Forward computationThe sequence of N complex numbers {x} is transformed into the sequence of N complex numbers {X} by the DFT according to the formula:
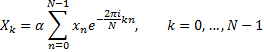
where i is the imaginary unit and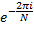 
is a primitive N'th root of unity. α denotes the forward scale factor.
The transform is sometimes denoted as follows:
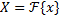
Backward computationThe inverse discrete Fourier transform (IDFT) is given by:
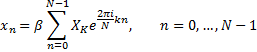
where β denotes the backward scale factor. If you want to get the initial sequence after applying forward and then backward transform you need to specify α and β such that α * β = 1/N. Generally, α = 1; β = 1/N, or α = β = 1/√N.
A simple description of these equations is that the complex numbers {X} represent the
amplitude and phase of the different sinusoidal components of the input "signal" {x}. The DFT computes
the {X} from the {x}, while the IDFT shows how to compute the {x} as a sum of sinusoidal components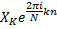 
with frequency k/N cycles per sample.
See Also