Correlations And Covariance |
Correlation and covariance methods provide measures of statistical relation between series data based on linear Pearson’s product-moment correlation coefficient.
Matrix columns correspond to variables, rows correspond to observations.
Hereinafter the following convention is used:
A, B denote matrices.
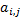denotes matrix elements, i = 0..n-1, j= 0..m-1.
Covariance is a measure of how much two variables change together.
Correlation coefficient is ranged from -1 to 1 and measures the extent to which values of two variables change "proportionally" to each other, i.e. as one variable increases, how much another variable tends to increase or decrease. The value of 1 represents a perfect positive correlation when both variables fluctuate around their means coherently, the value of -1 indicates exactly opposite tendency and the value of 0 represents a lack of correlation, i.e. linear statistical independence.
In case of matrix columns corresponds to variables and rows corresponds to observations. Thus for each column the corresponding operation is calculated analogically to vector case with each of the other columns. The resulting covariance or correlation will be then a matrix too. The given formulas show how elements of covariance and correlation matrices are calculated.
MethodsOperation | Description | Performance |
|---|---|---|
covariance | Returns population covariance. 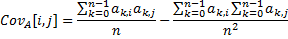 The following method calculates covariance and mean. | |
population covariance | Returns population covariance. 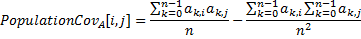 The following method calculates population covariance and mean. | |
sample covariance | Returns sample covariance. 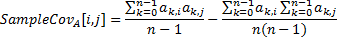 The following method calculates sample covariance and mean. | |
correlation | Returns correlation. 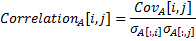 The following method calculates correlation and mean. | |
cross-covariance | Returns cross-covariance between two vector sets.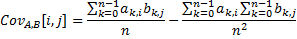 
The following method calculates cross-covariance and mean.
| |
cross-covariance sample | Returns sample cross-covariance between two vector sets.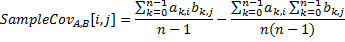 
The following method calculates cross-covariance and mean.
| |
cross-covariance population | Returns population cross-covariance between two vector sets, which is identical to simple cross-covariance between two vector sets.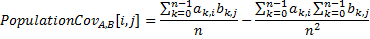 
The following method calculates cross-covariance and mean.
| |
cross-correlation | Returns cross-correlation between two vector sets. Cross-correlation matrix elements are correlation of the first matrix columns with the second matrix columns. 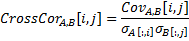 where the standard deviation of matrix A is computed as the standard deviation of the array A(:).
The following method calculates correlation and mean.
|
Code SampleThe example of correlation and crosscorrelation calculation:
1using System; 2using FinMath.LinearAlgebra; 3using FinMath.Statistics; 4 5namespace FinMath.Samples 6{ 7 class MatrixCorrelationSample 8 { 9 static void Main() 10 { 11 // Input parameters. 12 const Int32 xColumnsCount = 3; 13 const Int32 yColumnsCount = 2; 14 const Int32 observationsCount = 10; 15 16 // Generating input Matrix. 17 Matrix X = Matrix.Random(observationsCount, xColumnsCount); 18 Matrix Y = Matrix.Random(observationsCount, yColumnsCount); 19 Console.WriteLine("Transposed X matrix:"); 20 Console.WriteLine(X.GetTransposed().ToString("0.000")); 21 Console.WriteLine(); 22 Console.WriteLine("Transposed Y matrix:"); 23 Console.WriteLine(Y.GetTransposed().ToString("0.000")); 24 Console.WriteLine(); 25 26 // Compute and output X correlation matrix, i.e. correlation of X columns. 27 Console.WriteLine("X correlation matrix:"); 28 Console.WriteLine(X.Correlation().ToString("0.000")); 29 Console.WriteLine(); 30 // Compute and output Y correlation matrix, i.e. correlation of Y columns. 31 Console.WriteLine("Y matrix correlation (correlation of Y columns):"); 32 Console.WriteLine(Y.Correlation().ToString("0.000")); 33 Console.WriteLine(); 34 // Compute and output crosscorrelation between X and Y, i.e. correlation between X and Y columns. 35 Console.WriteLine("Crosscorelation between X and Y:"); 36 Console.WriteLine(X.CrossCorrelation(Y).ToString("0.000")); 37 } 38 } 39}
See Also