Basic Terms And Steps |
Genetic algorithm repeatedly modifies a family of individual solutions. At each step a probabilistic selection of certain individuals is made from the current parent generation, and a new generation then produced. "Еvolution" to the optimal solution happens through subsequent selection of generations.
Stochastic optimization refers to the minimization (or maximization) of a function in the presence of randomness in the optimization process. The randomness may be presented as either noise in measurements or Monte Carlo randomness in the search procedure, or both.
This topic contains the following sections:
Individual is a term that means any possible solution. Population is a group of all individuals. The space of all feasible solutions (it means objects among those the desired solution is) is called search space.
Selection is the stage of a genetic algorithm in which individuals are chosen from a population for later breeding (recombination or crossover).
Crossover takes parent solutions (mother and father) and creates a new offspring: one or two children.
After a crossover is performed, a mutation takes place. It is important to prevent falling of all solutions in population into a local optimum of solved problem. Mutation changes randomly the new offspring.
The fitness is the function you want to optimize. The fitness function is defined over the genetic representation and measures the quality of the represented solution.
Also you may think that making new population only by new offspring can cause loss of the best chromosome from the last population. This is true, so so-called elitism is often used. This means, that a specified percent of best solutions is copied without changes to a new population, so the best solution found can survive to end of run.
Genetic Algorithm flowchart:
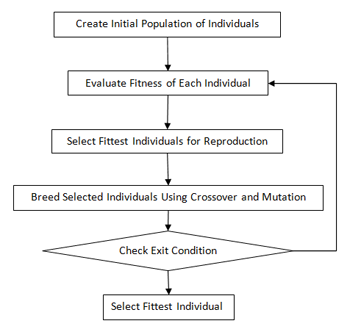
Creation
The population is generated randomly, covering the entire range of possible solutions (the search space). Occasionally, the solutions may be "seeded" in areas where optimal solutions are likely to be found.
Selection
Individuals are chosen from a population for later breeding.
The fitness function is evaluated for each individual, providing fitness values, which are then scaled. Scaling may be proportional to rank or to fitness value.
Selection types:
Uniform
Uniform selection chooses each individual with equal probability.
Stochastic Uniform
Stochastic uniform lays out a line in which each parent corresponds to a section of the line of length proportional to its scaled value. The algorithm moves along the line in steps of equal size. At each step, the algorithm allocates a parent from the section it lands on.
Roulette
Roulette selection chooses parents by simulating a roulette wheel, in which the area of the section of the wheel corresponding to an individual is proportional to the individual's scaled fitness. The algorithm uses a random number to select one of the sections with a probability equal to its area.
Tournament
Tournament selection chooses each parent by choosing 2 individual at random and then choosing the best individual out of that set to be a parent.
Crossover And Mutation
A pair of "parent" solutions is selected from the population to produce each child solution or two child solutions. Child solution usually shares many of the characteristics of its “parents”. New parents are selected for each new child, and the process continues until a new population of solutions of appropriate size is generated. Since only the best organisms from the first generation are selected for breeding, generally the average fitness will have increased by this procedure for the population.
Specific crossover made for a specific problem can improve performance of the genetic algorithm. Many crossover techniques exist for different data structures and encoding.
Mutation is a genetic operator dedicated to maintain genetic diversity from one generation of chromosomes to the next. The classic example of a mutation operator involves a probability that an arbitrary bit in a genetic sequence will be changed from its original state.
Mutation should allow the algorithm to avoid local minima by preventing the population of chromosomes from becoming too similar to each other, thus slowing or even stopping evolution.
This is how breeding happens:
Individuals are sorted by their fitness.
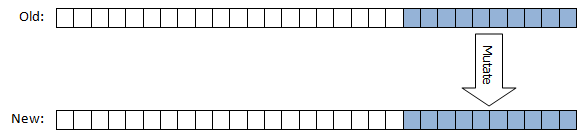
MutationPercent of the least fittest individuals are selected from last generation, mutated and moved to new generation. This can be illustrated in the following picture. Rank decreases from left to right, i.e. the most fittest individuals are at the left:
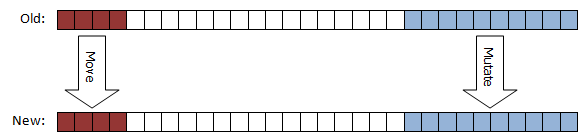
Min(100-MutationPercent, DominationPercent) individuals with highest rank are selected and moved directly to new generation:
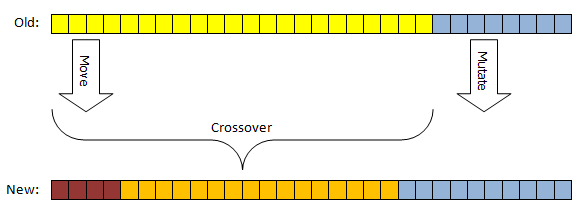
ElitismPercent best individuals are selected from old generation and until new generation is not filled up, two of ElitismPercent best individuals are selected, perform crossover and copied to new generation:
Termination
The iterations are repeated until a termination condition has been reached.
Common terminating conditions are:
Fixed number of generations reached
User specified exit condition is satisfied. For example, the solution satisfies minimum criteria, or the iterations no longer produce better results.