Implementation And Usage |
This topic contains the following sections:
Genetic Algorithm is implemented by the GeneticAlgorithmT class. The algorithm can be applied to a desirable data structure which implements the individual solutions of the problem. User should design methods implementing creation, crossover, mutation, fitness computing and if necessary, elitism and exit condition methods. These methods may significantly vary according to specific problem to be solved.
Delegates point to genetic functions, which implement creation, crossover, mutation, end condition check, elitism investigation and fitness calculation.
Function | Description | Performance |
|---|---|---|
creation | Creates a new individual. | |
one child crossover | Crossovers two individuals and produces one child. | |
two children crossover | Crossovers two individuals and produces two children. | |
mutation | Mutates individual. | |
exit condition | True, if algorithm has to stop. Otherwise, false. | |
objective | Calculates fitness value. | |
objective | Calculates multiple fitness values. | |
elitism | Investigates elitism for the given individual. |
The provided constructors create an instance of the Genetic Algorithm class. User may specify a delegate for exit condition check and elitism investigation.
Constructors may take one child or two children crossover delegate depending on the desirable crossover type.
Constructor | Description | Performance |
|---|---|---|
simple constructor | With one child crossover: With two children crossover: | |
block-oriented objective calculation | With one child crossover: With two children crossover: |
Genetic Algorithm class provides methods to run, stop and continue the algorithm execution.
Parameters are integral part of genetic algorithms and Genetic Algorithm class provides a wide range of adjustable parameters. User may set the parameters values which fit the problem and user requirents.
Parameter | Description | Performance |
|---|---|---|
population size | Population size of each generation. | |
selection algorithm | The selection algorithm, which can be Uniform Selection, Stochastic Uniform Selection , Roulette Selection or Tournament Selection. | |
selection function type | Defines selection probability function distribution type: Uniform, Stochastic Uniform, Roulette or Tournament. This function defines the selection algorithm, which will be used in case the selection algorithm is not user-defined. | |
random generator | This is the random generator which is used for population creation, crossover and mutation. | |
generations count | Number of generations algorithm will make. | |
elitism percent | Percent of population selected for crossover (0-100). | |
mutation percent | Percent of next population that will be mutated. | |
domination percent | Percent of population that will be left intact. | |
fitness scaling | Fitness scaling type: Rank or Proportional. | |
tournament size | Tournament size for tournament selection. |
Statistics help analyze the algorithm efficiency and get the fittest individuals.
Statistic | Description | Performance |
|---|---|---|
population | Array of all individuals in current population. | |
best objective | Objective of the best individual from current population. | |
best individual | The best individual from current population. | |
size of elite | Size of elite of current generation. | |
generation number | Current generation number. |
This section presents an example that shows how to find the minimum of Rastrigin's function, a function that is often used to test the genetic algorithm. For two independent variables, Rastrigin's function is defined as follows:
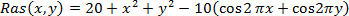
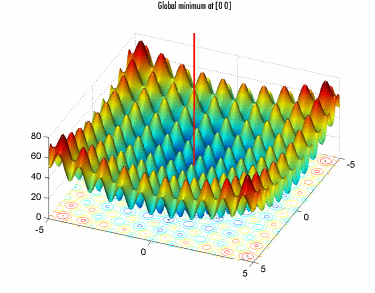
The following figure shows a plot of Rastrigin's function:
The following code implements the genetic algorithm class functionality:
1using System; 2using FinMath.MachineLearning.EvolutionaryAlgorithms; 3using FinMath.Statistics; 4 5namespace FinMath.Samples 6{ 7 class GeneticAlgo 8 { 9 // Chromosomes for this task represents two dimensional Rastrigin function arguments. 10 public class RastriginArguments 11 { 12 public double x, y; 13 } 14 15 // Domain boundaries. 16 static double Min, Max; 17 18 static void Main() 19 { 20 const Int32 stepCount = 25; 21 const Int32 populationSize = 50000; 22 Min = -10; 23 Max = 10; 24 25 // Initialize new genetic algorithm class instance. 26 GeneticAlgorithm<RastriginArguments> ga = new GeneticAlgorithm<RastriginArguments>(Creation, Crossover, Mutation, RastriginFunction); 27 28 // Set GA to make only one generation. 29 ga.PopulationSize = populationSize; 30 31 // Perform one step of Genetic Algorithm. 32 // You can set generation count to anything you want and call "Run" method to make arbitrary number of steps. 33 ga.GenerationsCount = 1; 34 ga.Run(); 35 for (Int32 i = 0; i < stepCount; ++i) 36 { 37 // Continue optimization process. 38 ga.Continue(); 39 // Get best solution candidate. 40 RastriginArguments best = ga.Population[0]; 41 42 // Output the coordinates of minimum of the function. 43 Console.WriteLine($"{i:00}: x = {best.x:0.00000}, y = {best.y:0.00000} value = {ga.BestObjective:0.00000}"); 44 } 45 } 46 47- #region Rastrigin routines 48 49 // Return Rastrigin function individual. 50 public static RastriginArguments Creation(RandomGenerator r) 51 { 52 double tx = r.NextDouble(Min, Max); 53 double ty = r.NextDouble(Min, Max); 54 55 return new RastriginArguments { x = tx, y = ty }; 56 } 57 58 // Perform a crossover (child X = parents X coordinates sum divided by 2). 59 public static void Crossover(RastriginArguments mother, RastriginArguments father, ref RastriginArguments child, RandomGenerator r) 60 { 61 child.x = (mother.x + father.x) / 2; 62 } 63 64 // Mutate this individual (value of x coordinate is selected randomly). 65 public static void Mutation(ref RastriginArguments t, RandomGenerator r) 66 { 67 if (r.Next(2) == 0) 68 t.x = r.NextDouble(Min, Max); 69 else 70 t.y = r.NextDouble(Min, Max); 71 } 72 73 // Fitness is the Rastrigin function value. 74 public static double RastriginFunction(RastriginArguments t) 75 { 76 Double x = t.x; 77 Double y = t.y; 78 79 return 20 + Math.Pow(x, 2) + Math.Pow(y, 2) - 10 * (Math.Cos(2 * Math.PI * x) + Math.Cos(2 * Math.PI * y)); 80 } 81 #endregion 82 } 83}


