Constrained Optimization

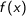A constrained optimization problem is a regular constraint satisfaction problem augmented with an objective function to be minimized (or maximized). A general constrained optimization problem with respect to vector argument of the objective function may be written as:

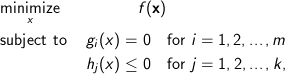
where .

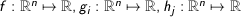Constraints 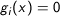are usually called equality constraints, and constraints 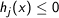- inequality constraints.

If functions 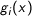or 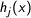is linear, the corresponding constraint is called linear equality constraints and linear inequality constraint respectively. Linear constraints are the most common and the most popular constraints. Linear inequality constraints are usually subdivided into bound constraints and common inequality constraints. Thus there are three kind of linear constraints:

• Linear equality constraints:

  

• Linear inequality constraints:

  

• Bound constraints:

  

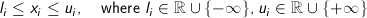
Also several constraint of the same type can be grouped. Thus linear constraints may be written in the following general form:

IConstrainedProgramming contains common fields for all constrained optimization algorithms. This interface exposes a set of properties: