Linear Programming |
This topic contains the following sections:
Linear Programming Problem SpecificationGeneral form of linear programming problem has the form:
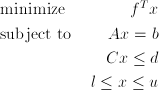
where
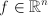- linear objective function vector,
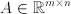- matrix for linear equality constraints,
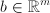- vector for linear equality constraints,
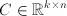- matrix for linear inequality constraints,
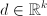- vector for linear inequality constraints,
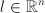- vector of lower bounds,
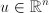- vector of upper bounds.
Implementation and UsageThe linear programming solver implements a variant of Mehrotra's predictor-corrector algorithm, a primal-dual interior-point method. A number of preprocessing steps occur before the algorithm begins to iterate. The linear programming solver is implemented by the LinearProgramming class. The following constructors create an instance of this class:
The class implements the IConstrainedProgramming interface.
Constructor | Description | Performance |
|---|---|---|
A and C - dense matrices | Creates new instance of LinearProgramming class.
| |
A and C - sparse matrices | Creates new instance of LinearProgramming class.
|
The class implements an event LogMessage that occurs every time the INumericalOptimization wants to send a log message, and the following methods:
Method | Description | Performance |
|---|---|---|
minimum | Finds minimum of constrained multivariable function and returns true in case the optimization algorithm succeeded. | |
minimum with initial point provided | Finds minimum of constrained multivariable function and returns true in case the optimization algorithm succeeded. The initial point for the algorithm is passed as a parameter. |
Class provides the following properties:
Property | Description | Performance |
|---|---|---|
iterations done | Number of iterations done. | |
iterations limit | Maximum number of iterations allowed, a positive integer. | |
minimum point | Minimum point of objective function. | |
minimum value | Minimum value of objective function. | |
status | Status of algorithm termination. | |
tolerance | Algorithm termination tolerance, a positive scalar. |
 Note |
|---|
Usually the default tolerance settings provide good convergence so there is no need to adjust them. |
Code SampleThe example demonstrate how to determine input parameters in standard form and use the LP solver for the following problem:
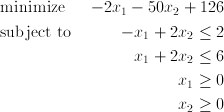
To present this problem in the standard form, there should be:
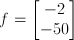
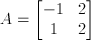
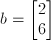
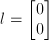
The following code solves the problem:
1using System; 2using FinMath.LinearAlgebra; 3using FinMath.NumericalOptimization.Constrained; 4 5namespace FinMath.Samples 6{ 7 class LinearProgrammingSample 8 { 9 static void Main() 10 { 11 // Objective function. 12 Vector F = new Vector(new Double[] { -2.0, -50.0 }); 13 14 // Linear inequality constraints. 15 Matrix Ai = new Matrix(new Double[,] { { -1.0, 2.0 }, { 1.0, 2.0 } }); 16 Vector Bi = new Vector(new Double[] { 2.0, 6.0 }); 17 18 // Lower bounds on variables. 19 Vector L = new Vector(new Double[] { 0.0, 0.0 }); 20 21 // Create an instance of the solver. 22 LinearProgramming solver = new LinearProgramming(F, null, null, Ai, Bi, L, null); 23 24 // Setting of the solver. 25 solver.Tolerance = 1.0E-8; 26 solver.IterationsLimit = 50; 27 28 // Delegate used to print messages. 29 solver.LogMessage += Console.WriteLine; 30 31 // Find minimum. 32 solver.Minimize(); 33 34 // Get minimum point. 35 if (solver.Status == FMStatus.MethodSucceeded) 36 { 37 Console.WriteLine("MinimumPoint = " + solver.MinimumPoint.ToString("")); 38 } 39 else 40 { 41 Console.WriteLine("Linear programming solver failed."); 42 } 43 } 44 } 45}
See Also