Matrix Normal

The matrix normal distribution is a probability distribution that is a generalization of the normal distribution to matrix-valued random variables.

Distribution parameters are mean matrix M, row covariance matrix Ω and column covariance matrix Σ.

This topic contains the following sections:

Constructors

Constructor	Description	Performance
set M, Ω and Σ	Creates new instance of MatrixNormal with user specified parameters. MatrixNormal(Matrix, Matrix, Matrix)
set M, Ω, Σ and random generator	Creates new instance of MatrixNormal with user specified parameters. MatrixNormal(RandomGenerator, Matrix, Matrix, Matrix)

Constructor

Description

Performance

set M, Ω and Σ

Creates new instance of MatrixNormal with user specified parameters.

set M, Ω, Σ and random generator

Creates new instance of MatrixNormal with user specified parameters.

Methods

Method	Description	Performance
sample	Generate random variable sample. In place: Sample(Matrix) Returning result: Sample(Matrix, Matrix, Matrix) Sample(RandomGenerator, Matrix, Matrix, Matrix)
pdf	Probability density function. Pdf(Matrix) Pdf(Matrix, Matrix, Matrix, Matrix)

Method

Description

Performance

sample

Generate random variable sample.

pdf

Probability density function.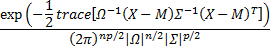

Properties

Property	Description	Performance
mean	Means matrix. Mean
row covariance	Row covariance matrix. RowCovariance
column covariance	Column covariance matrix. ColumnCovariance
is row covariance positive definite	Indicates whether user specified row covariance matrix is positive definite. RowCovarianceIsPositiveDefinite
is column covariance positive definite	Indicates whether user specified column covariance matrix is positive definite. ColCovarianceIsPositiveDefinite