Inverse Wishart

The inverse Wishart distribution, also called the inverted Wishart distribution, is a probability distribution defined on real-valued positive-definite matrices.

We say B follows an inverse Wishart distribution, if its inverse matrix has a Wishart distribution.

Inverse Wishart distribution parameters are inverse scale matrix Ψ and number of degrees of freedom m.

This topic contains the following sections:

Constructors
Methods
Properties

Constructors

Constructor	Description	Performance
set inverse scale matrix Ψ and degrees of freedom m	Creates new instance of InverseWishart with user specified parameters. InverseWishart(Matrix, Double)
set Ψ, m and random generator	Creates new instance of InverseWishart with user specified parameters. InverseWishart(RandomGenerator, Matrix, Double)

Constructor

Description

Performance

set inverse scale matrix Ψ and degrees of freedom m

Creates new instance of InverseWishart with user specified parameters.

method InverseWishart(Matrix, Double)

set Ψ, m and random generator

Creates new instance of InverseWishart with user specified parameters.

method InverseWishart(RandomGenerator, Matrix, Double)

Methods

Method	Description	Performance
sample	Generate random variable sample. In place: Sample(Matrix) Returning result: Sample(Matrix, Double) Sample(RandomGenerator, Matrix, Double)
pdf	Probability density function. 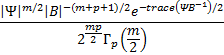where p is the order of the matrix Ψ, and Γ is the multivariate gamma function. Pdf(Matrix) Pdf(Matrix, Matrix, Double)

Method

Description

Performance

sample

Generate random variable sample.

In place:

method Sample(Matrix)

Returning result:

Static Sample(Matrix, Double)

Static Sample(RandomGenerator, Matrix, Double)

pdf

Probability density function.

where p is the order of the matrix Ψ, and Γ is the multivariate gamma function.

method Pdf(Matrix)

Static Pdf(Matrix, Matrix, Double)

Properties

Property	Description	Performance
inverse scale	Inverse scale matrix. InverseScale
degrees of freedom	Number of degrees of freedom. DegreesOfFreedom
mean	Means matrix. 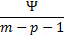Mean
mode	Modes matrix. 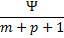Mode
generation method	Method of normal distribution generation. See Normal Method