Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm

As any of Newton-like methods, BFGS uses quadratic Taylor approximation of the objective function in a d-vicinity of x:

f(x + d) ≈ q(d) = f(x) + d^Tg(x) + ½ d^TH(x) d,

where g(x) is the gradient vector and H(x) is the Hessian matrix.

The necessary condition for a local minimum of q(d) with respect to d results in the linear system:

g(x)+ H(x) d = 0

which, in turn, gives the Newton direction d for line search:

d = - H(x)^-1g(x))

The exact Newton direction (which is subject to define in Newton-type methods) is reliable when

• The Hessian matrix exists and positive definite;

• The difference between the true objective function and its quadratic approximation is not large.

In Quasi–Newton methods, the idea is to use matrices which approximate the Hessian matrix and/or its inverse, instead of exact computing of the Hessian matrix (as in Newton-type methods). The matrices are normally named B ≈ H and D ≈ H ^-1.

The matrices are adjusted on each iteration and can be produced in many different ways ranging from very simple techniques to highly advanced schemes.

The BFGS method uses the BFGS updating formula which converges to H (x^*):

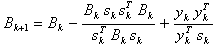
• s_k = x_k+1 - x_k,

• y_k = g_k+1 - g_k.

The BFGS method exposes superlinear convergence; resource-intensivity is estimated as O(n²) per iteration for n-component argument vector.

The BFGS algorithm is implemented by the BFGS class. The implementation realizes two-stage iterative process according to general line search strategy:

• 'Outer' iterations define BFGS-based line search direction;

• 'Inner' iterative process solves the step length subproblem using either the default (Strong Wolfe) approach or user-specific implementation.

To initialize an instance of the class use one of the two constructors provided, both the constructors require objective function and its gradient to be presented as delegate methods:

• BFGS(Int32, QuasiNewtonFunctionDelegate, QuasiNewtonGradientDelegate)

• BFGS(Int32, QuasiNewtonFunctionDelegate, QuasiNewtonGradientDelegate, LineSearch)

The BFGS optimizer is controlled by stopping criteria and one more parameter as class properties that have default values assigned while initialization and should be customized (if necessary) before running of optimization process; the default values are suitable in most practical applications:

The following class properties present optimization results:

The sample demonstrates BFGS-minimization of Rosenbrock function:

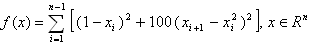
Gradient of this function is:

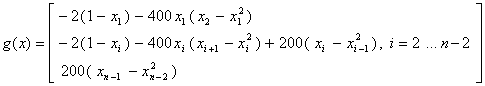
Both function and its gradient should be presented as delegate methods.

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.NumericalOptimization.Unconstrained;
 4
 5namespace FinMath.Samples
 6{
 7    class BFGSOptimization
 8    {
 9        static void Main()
10        {
11            //Domain dimension (the number of arguments of the objective function).
12            Int32 n = 3;
13
14            // Initialize BFGS optimizer for Rosenbrock function.
15            BFGS bfgs = new BFGS(n, RosenbrockFunction, RosenbrockGradient);
16
17            // Define start point.
18            Vector startPoint = Vector.Random(n);
19            Console.WriteLine($"Start Point = {startPoint.ToString("0.000000")}");
20
21            // Set up stopping criteria (if necessary).
22            bfgs.ArgumentTolerance = 1.0E-9;
23            bfgs.FunctionTolerance = 1.0E-9;
24            bfgs.IterationsLimit = 1000;
25
26            // Run the optimization.
27            bfgs.Minimize(startPoint);
28
29            // Check computation status and get results.
30            if (bfgs.Status == FMStatus.MethodSucceeded)
31            {
32                Console.WriteLine($"Minimum Point = {bfgs.MinimumPoint.ToString("0.000000")}");
33                Console.WriteLine($"Objective Function = {RosenbrockFunction(bfgs.MinimumPoint):0.000000}");
34                Console.WriteLine();
35                Console.WriteLine($"Iterations Done = {bfgs.IterationsDone}");
36            }
37            else
38            {
39                Console.WriteLine($"BFGS failed with status {bfgs.Status}");
40            }
41        }
42
43        private static Double RosenbrockFunction(Vector x)
44        {
45            Int32 n = x.Count;
46            Double y = 0.0;
47            for (Int32 i = 0; i < n - 1; i += 1)
48            {
49                y += Math.Pow((1.0 - x[i]), 2.0) + 100.0 * Math.Pow((x[i + 1] - Math.Pow(x[i], 2.0)), 2.0);
50            }
51            return y;
52        }
53
54        private static void RosenbrockGradient(Vector x, Vector g)
55        {
56            Int32 n = x.Count;
57
58            g[0] = -2.0 * (1.0 - x[0]) - 400.0 * (x[1] - Math.Pow(x[0], 2.0)) * x[0];
59            g[n - 1] = 200.0 * (x[n - 1] - Math.Pow(x[n - 2], 2.0));
60
61            for (Int32 i = 1; i < n - 1; i += 1)
62            {
63                g[i] = -2.0 * (1.0 - x[i]) - 400.0 * (x[i + 1] - Math.Pow(x[i], 2.0)) * x[i] + 200.0 * (x[i] - Math.Pow(x[i - 1], 2.0));
64            }
65        }
66    }
67}

Reference

Other Resources