Negative Binomial

The negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified (non-random) number r of failures occurs.

Suppose there is a sequence of independent Bernoulli trials, each trial having two potential outcomes called “success” and “failure”. In each trial the probability of success is p and of failure is (1 − p). We are observing this sequence until a predefined number r of failures has occurred. Then the random number of successes we have seen, X, will have the negative binomial distribution:

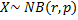
This topic contains the following sections:

Constructor
Methods
Properties

Constructor

Constructor	Description	Performance
set success probability and number of failures	Creates new instance of NegativeBinomial with user specified parameters. NegativeBinomial(Int32, Double)
set random generator	Creates new instance of NegativeBinomial with user specified parameters and generator. NegativeBinomial(RandomGenerator, Int32, Double)

Description

Performance

set success probability and number of failures

Creates new instance of NegativeBinomial with user specified parameters.

method NegativeBinomial(Int32, Double)

set random generator

Creates new instance of NegativeBinomial with user specified parameters and generator.

method NegativeBinomial(RandomGenerator, Int32, Double)

Methods

Method	Description	Performance
sample	Generate random variable sample. Sample Fill in array with random variable series in place: Sample(Int32) Static method which generates new sample of negative binomial distribution variate with specified parameters: Sample(Int32, Double) Sample(RandomGenerator, Int32, Double)
pmf	Probability mass function. 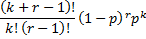Pmf(Int32) Static probability mass function. Pmf(Int32, Int32, Double)
cdf	Cumulative distribution function. 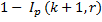Cdf(Int32) Static cumulative distribution function. Cdf(Int32, Int32, Double)
inverse cdf	Inverse cumulative distribution function. Is useful for quantile calculation. Function will return value of random variable such that likelihood for this random variable to occur less than or equal to returned value equal to specified pvalue parameter. InverseCdf(Double, Int32, Double)

Properties

Property	Description	Performance
number of failures	Number of failures until the experiment is stopped. NumberOfFailures
success probability	Success probability in each trial. SuccessProbability
mean	Mean of the distribution. 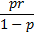Mean
mode	Mode of distribution. 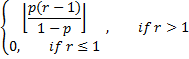Mode
kurtosis	Excess Kurtosis of distribution. 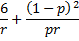Kurtosis
skewness	Skewness of distribution. 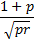Skewness
variance	Variance of the distribution. 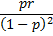Variance