Geometric |
Discrete univariate (shifted) geometric distribution is the probability distribution of the number X of Bernoulli trials needed to get one success, supported on the set { 1, 2, 3, ...}.
It’s the probability that the first occurrence of success require k number of independent trials, each with success probability p. If the probability of success on each trial is p, then the probability that the k'th trial (out of k trials) is the first success is
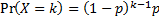
for k = 1, 2, 3, ....
This topic contains the following sections:
ConstructorConstructor | Description | Performance |
|---|---|---|
set success probability | Creates new instance of Geometric with user specified success probability. |
MethodsMethod | Description | Performance |
|---|---|---|
pmf | Probability mass function. 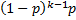 Static probability mass function. | |
cdf | Cumulative distribution function. 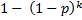 Static cumulative distribution function. | |
inverse cdf | Inverse cumulative distribution function. Is useful for quantile calculation. Function will return value of random variable such that likelihood for this random variable to occur less than or equal to returned value equal to specified pvalue parameter. |
PropertiesProperty | Description | Performance |
|---|---|---|
success probability | Success probability in each trial p. | |
mean | Mean of the distribution.  | |
median | Median is the numerical value separating the higher half of a probability distribution, from the lower half.  | |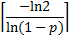
mode | Mode of distribution.  | |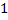
kurtosis | Excess Kurtosis of distribution.  | |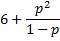
skewness | Skewness of distribution.  | |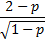
entropy | Entropy of the distribution.  | |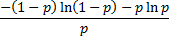
variance | Variance of the distribution.  |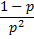
