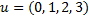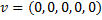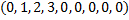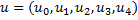Extensions |
Hereinafter the following convention is used:
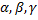– small Greek letters are used to denote scalars;
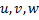– small Latin letters are used to denote vectors;
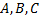– capital Latin letters are used to denote matrices.
ConcatenationThis section describes methods applied to concatenate two vectors. Concatenation is the joining of two vectors in one vector.
Operation | Description | Performance |
|---|---|---|
concatenate | Concatenates two given vectors. Consider we have vectors:
The result will be |
PermutationPermutation is a procedure that changes order of vector elements. User specifies the sequence, in which the elements of the vector will be placed after the permutation. Obviously, the specified array must have the same number of elements as the given vector.
Operation | Description | Performance |
|---|---|---|
permutation | Permutes elements of the vector. |
Useful RoutinesThis section describes some other useful methods.
Operation | Description | Performance |
|---|---|---|
clear the vector | Sets all elements of this vector to zero. | |
normalize | Divides each element of the vector onto the norm.  | |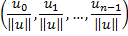
negate | Negates all elements of this vector.  | |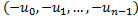
add scaled vector | Adds another vector multiplied by given scalar to this one.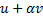 
| |
matrix-vector product | Computes the matrix-vector product in general form. It multiplies this vector u by scalar β and adds product of matrix and vector v scaled by another scalar α. 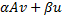 User may specify if the matrix should be transposed or not with boolean parameter: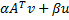 
|
See Also