Dirichlet |
The Dirichlet distribution, often denoted Dir(α), is a family of continuous multivariate probability distributions parametrized by a vector α of k positive reals. It is the multivariate generalization of the beta distribution.
Dirichlet distribution gives the probability of choosing a given collection of m items from a set of k items with repetitions and the number of observations of each choice given by vector α.
This topic contains the following sections:
ConstructorsConstructor | Description | Performance |
|---|---|---|
set vector α | Creates new instance of Dirichlet with user specified parameters. | |
set vector α and random generator | Creates new instance of Dirichlet with user specified parameters. | |
set double α and dimension | Creates new instance of Dirichlet representing symmetric distribution (same α for all variables). | |
set double α, dimension and random generator | Creates new instance of Dirichlet representing symmetric distribution (same α for all variables) with user specified random generator. |
MethodsMethod | Description | Performance |
|---|---|---|
sample | Generates random variable sample. Generates series of random variable samples. | |
Probability density function. 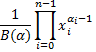 where B is the multinomial beta function. Note: xi>0 and Σxi=1 otherwise pdf equals 0. |
PropertiesProperty | Description | Performance |
|---|---|---|
mean | Mean of the distribution.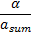 
where | |
mode | Mode of the distribution.  | |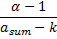
variance | Variance of the distribution.  | |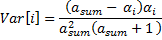
covariance | Covariance matrix of the distribution.  |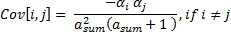
