Multivariate |
Multivariate distribution encompasses the simultaneous observation of more than one statistical variable. A continuous multivariate distribution is a probability distribution of variables each of which is characterized by a probability density function. Multivariate distribution sample is an array or vector of each variable single observation. The series of samples is a matrix, columns correspond to variables and rows correspond to observations.
Among the most well-known multivariate probability distributions that are used for statistical modeling are:
This topic contains the following sections:
An abstract class CVDistribution represents base continuous multivariate distribution.
All subclasses inherit from this class the following methods:
Method | Description | Performance |
|---|---|---|
sample | Generate random variable sample. In place:Returning result:Generate series of random variable samples. In place:Returning result: | |
Probability density function. 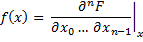 where F is a cumulative distribution function of the vector of variables. | ||
cdf | Cumulative distribution function. 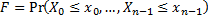 |
All subclasses inherit from this class the following properties:
Property | Description | Performance |
|---|---|---|
dimension | Dimension of the distribution. | |
mean | Mean of the distribution. | |
mode | The value that occurs most frequently in a probability distribution. | |
entropy | A measure of the uncertainty associated with random variables. | |
variance | A measure of how far a set of numbers are spread out from each other. 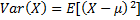 | |
covariance | Covariance matrix of the distribution. 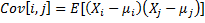 where μi = E(Xi) is the expected value of the i-th variable. |

