Moments and Derivatives |
In statistics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. Moments include raw moments and central moments.
Hereinafter the following convention is used:
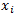 denotes data container element, i = 0..n-1. For vector, array of doubles and array of nullable doubles
denotes data container element, i = 0..n-1. For vector, array of doubles and array of nullable doubles 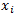 denotes an array element or vector element.
denotes an array element or vector element.
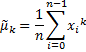
Thus, the first moment of the vector or array elements is the expectation operator, i.e., the mean of the data set.
The central moments (moments about the mean) are more interesting than the moments about zero. The k-th central moment of data set is:
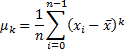
The skewness measures deviation of a distribution from symmetry around the mean so that the value near to zero points out perfect symmetry when the Mean and the Median are almost equal; negative values for the Skewness indicate data that are skewed left so the Mean is less than the Median and vice versa.
The kurtosis (also known as excess kurtosis) is a measure of whether the data are peaked or flat relative to normal distribution and this way characterizes the shape of a distribution: the kurtosis of the normal distribution is zero by definition; if the kurtosis is negative then the distribution is flatter (observations are spread in a wider fashion) than normal and vice versa. Its value does not depend on an arbitrary change of the scale and location of the distribution.
The coefficient of variation (also known as unitized risk or the variation coefficient) allows measuring dispersion relative to the expected value. It is a useful statistic for comparing the degree of variation from one data series to another, even if the means are significantly different from each other. In mathematical sense, it is defined as the standard deviation normalized by the mean, i.e. as the ratio of the standard deviation to the arithmetic mean.
Operation | Description | Performance |
|---|---|---|
first raw moment | Returns first raw moment of the container's values. 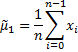
| |
second raw moment | Returns second raw moment of the container's values. 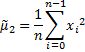
| |
third raw moment | Returns third raw moment of the container's values. 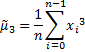
| |
fourth raw moment | Returns fourth raw moment of the container's values. 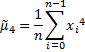
| |
second central moment | Returns second central moment of the container's values. 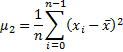
| |
third central moment | Returns third central moment of the container's values. 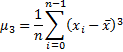
| |
fourth central moment | Returns fourth central moment of the container's values. 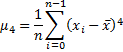
| |
skewness | Returns skewness of the container's values. 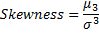 | |
kurtosis | Returns kurtosis of the container's values. 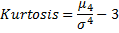 | |
coefficient of variation | Returns coefficient of variation of the container's values. 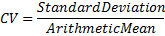
|
The following sample shows how to use moments:
1using System; 2using FinMath.LinearAlgebra; 3using FinMath.Statistics; 4 5namespace FinMath.Samples 6{ 7 class VectorMomentsSample 8 { 9 static void Main() 10 { 11 // Input parameters. 12 const Int32 observationsCount = 10; 13 14 // Generate input vector. 15 Vector vector = Vector.Random(observationsCount); 16 Console.WriteLine("Input vector:"); 17 Console.WriteLine(" " + vector.ToString("0.000")); 18 19 // Calculate and output different types of statistics. 20 Console.WriteLine("Results:"); 21 Console.WriteLine(" Second raw moment: " + vector.SecondRawMoment().ToString("0.00000")); 22 Console.WriteLine(" Second central moment: " + vector.SecondCentralMoment().ToString("0.00000")); 23 Console.WriteLine(" Skewness: " + vector.Skewness().ToString("0.00000")); 24 Console.WriteLine(" Kutosis: " + vector.Kurtosis().ToString("0.00000")); 25 Console.WriteLine(" Coefficient of variation: " + vector.CoefficientOfVariation().ToString("0.00000")); 26 } 27 } 28}
