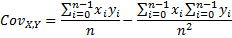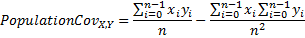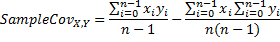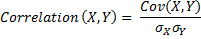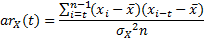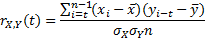Correlation and Covariance

Correlation and covariance methods provide measures of statistical relation between series data based on linear Pearson’s product-moment correlation coefficient.

Hereinafter the following convention is used:

X, Y denote data container, i.e. a vector or an array of doubles.

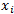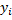, denote data container element, i = 0..n-1. For vector, array of doubles and array of nullable doubles it is an array element or vector element.

Covariance is a measure of how much two variables change together.

Correlation coefficient is ranged from -1 to 1 and measures the extent to which values of two variables change "proportionally" to each other, i.e. as one variable increases, how much another variable tends to increase or decrease. The value of 1 represents a perfect positive correlation when both variables fluctuate around their means coherently, the value of -1 indicates exactly opposite tendency and the value of 0 represents a lack of correlation, i.e. linear statistical independence. Although Correlation Coefficient is sensitive only to a linear relationship between two variables, it can also (not necessarily) point out a nonlinear relationship between the variables. The same formula applied to one variable X and describing the correlation between values of the variable at different time points (i.e. the correlation of the variable against a time-shifted version of itself) is called autocorrelation coefficient or cross-correlation coefficient.

The correlation and autocorrelation coefficients are commonly used for checking randomness in data series, to visualize correlations often correlogram and autocorellogram are used, that are spectrum-like plots of correlation coefficients at varying time lags.