Continious Univariate |
A continuous univariate distribution is a probability distribution of a single variable characterized by a probability density function. If X is a continuous random variable, then it has a probability density function ƒ(x), and therefore its probability to fall into a given interval, say [a, b] is given by the integral
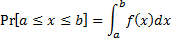
Among the most well-known continuous probability distributions that are used for statistical modeling are:
This topic contains the following sections:
An abstract class CUDistribution represents base continuous univariate distribution.
All subclasses inherit from this class the following methods:
Method | Description | Performance |
|---|---|---|
sample | Generates random variable sample. Generate series of random variable samples. In place:Returning result: | |
Probability density function. 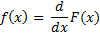 where F(x) is a cumulative distribution function. | ||
cdf | Cumulative distribution function. 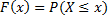 | |
inverse cdf | Inverse cumulative distribution function. 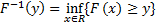 Is useful for quantile generation. Function will return random variable value such that probability that distribution sample will get value less than or equal to returned value is equal to specified probability. |
All subclasses inherit from this class the following properties:
Property | Description | Performance |
|---|---|---|
mean | Mean of the distribution. | |
median | Median is the numerical value separating the higher half of a probability distribution, from the lower half. | |
mode | The value that occurs most frequently in a probability distribution. | |
kurtosis | A measure of the "peakedness" of the probability distribution of a real-valued random variable. 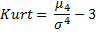 | |
skewness | A measure of the asymmetry of the probability distribution. 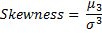 | |
entropy | A measure of the uncertainty associated with a random variable. | |
variance | A measure of how far a set of numbers are spread out from each other. 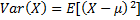 | |
standard deviation | A measure of variability or diversity. 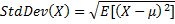 |

