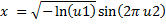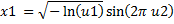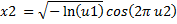Normal

The normal (or Gaussian) distribution is a continuous probability distribution that is often used as a first approximation to describe real-valued random variables that tend to cluster around a single mean value. The graph of the associated probability density function is “bell”-shaped, and is known as the Gaussian function or bell curve. It has two parameters: parameter μ is the mean (location of the peak) and σ is the standard deviation.

This topic contains the following sections:

Constructor
Methods
Properties

Constructor

Constructor	Description	Performance
set mean and standard deviation	Creates new instance of Normal with user specified parameters. Normal(Double, Double)
default mean and standard deviation	Creates new instance of Normal with default parameters (0; 1). Normal
set random generator	Creates new instance of Normal with user specified generator and parameters. Normal(RandomGenerator, Double, Double)

Description

Performance

set mean and standard deviation

Creates new instance of Normal with user specified parameters.

method Normal(Double, Double)

default mean and standard deviation

Creates new instance of Normal with default parameters (0; 1).

method Normal

set random generator

Creates new instance of Normal with user specified generator and parameters.

method Normal(RandomGenerator, Double, Double)

Methods

Method	Description	Performance
sample	Generate random variable sample. Sample Fill in array with random variable series in place: Sample(Double) Static method which generates new sample of Exponential distribution variate with specified parameters: Sample(Double, Double) Sample(RandomGenerator, Double, Double)
pdf	Probability density function. 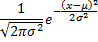Pdf(Double) Static probability density function. Pdf(Double, Double, Double)
cdf	Cumulative distribution function. 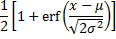where erf denotes the error function. Cdf(Double) Static cumulative distribution function. Cdf(Double, Double, Double)
inverse cdf	Inverse cumulative distribution function. Is useful for quantile calculation. Function will return value of random variable such that likelihood for this random variable to occur less than or equal to returned value equal to specified pvalue parameter. InverseCdf(Double) InverseCdf(Double, Double, Double)

Properties

Property	Description	Performance
mean	Mean of the distribution. 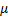Mean
median	Median of the distribution. 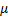Median
mode	Mode of distribution. 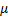Mode
kurtosis	Excess Kurtosis of distribution. 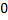Kurtosis
skewness	Skewness of distribution. 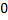Skewness
entropy	Entropy of distribution. 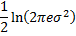Entropy
variance	Variance of the distribution. 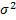Variance
standard deviation	Standard deviation of the distribution. 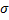StandardDeviation
method	Method of normal distribution generation. Method may take values: BOXMULLER generates normally distributed random number x through the pair of uniformly distributed numbers u1 and u2 according to the formula: BOXMULLER2 generates normally distributed random numbers x1 and x2 through the pair of uniformly distributed numbers u1 and u2 according to the formulas: and Inverse cumulative distribution function method. Method