Principal Component Analysis (PCA)

PCA analyzes the relationship between the n observations of m variables. The central point of PCA is redefinition of this data set in terms of a new set of variables (Principal Components) which are mutually-orthogonal linear combinations of the original variables.

Formal specification and procedure is as follows:

Given a n-by-m data matrix X containing m variables-columns X _j , each presented by n observations in rows, should find such a line OY ₁ in the m-dimensional space that the variance of n observations projected onto this line is a maximum.

The derived line is called the first Principal Component of the data system and presented in linear form:

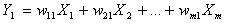
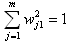Same procedure applied to (m-1)-dimensional subspace orthogonal to the Y₁, results in the the second Principal Component in this subspace. The process is continued until m mutually orthogonal lines are determined in form of m-by-m transformation matrix W of the coefficients w_jk , and this process is called Principal Components Analysis.

Robust computational approach to solve PCA is based on the Karhunen–Loeve transform, which states that the unknown matrix W of PCA transformation is equivalent to the matrix of eigenvectors of the covariance matrix C computed over the centered original data matrix. Thus, solving PCA is the two-stage procedure:

1. Centering of the original data matrix X around column means and computing the m-by-m covariance matrix C.

2. Computing the eigenvectors of the matrix C and getting the eigenvalues according to the equation:

   V ^-1 C V = D,

   where columns of V are the eigenvectors and D is the diagonal matrix of eigenvalues of C, each eigenvector corresponds to its eigenvalue.

The PCA method is implemented by the PCA class which utilizes the Karhunen–Loeve approach.

The class realizes the basic interface and extends it with useful properties.

To initialize an instance of the class use one of the two constructors provided:

• PCA(Matrix)

• PCA(Matrix, Int32)

Being successfully initialized (i.e. with the Status value equal to MethodSucceeded), the instance of the class is ready to perform direct (inverse) transformations of any set of input (transformed) observations with the methods of basic interface

Extensions of basic interface provide method-specific and convenience details as properties:

The example of PCA class usage:

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.FactorAnalysis;
 4
 5namespace FinMath.Samples
 6{
 7    class PCASample
 8    {
 9        static void Main()
10        {
11            // Input parameters.
12            const Int32 observationsCount = 8;
13            const Int32 seriesCount = 5;
14            const Double coverage = 0.9;
15
16            // Generate input matrix.
17            Matrix dataMatrix = Matrix.Random(observationsCount, seriesCount);
18            Console.WriteLine("Input data matrix:");
19            Console.WriteLine(dataMatrix.ToString("0.000"));
20            Console.WriteLine();
21
22
23            // Calculate PCA.
24            PCA pca = new PCA(dataMatrix);
25
26            if (pca.Status == FMStatus.MethodSucceeded)
27            {
28                Console.WriteLine("PCA calculated successfully.");
29
30                // Get PCA cumulative energy.
31                Vector energy = pca.CumulativeEnergy;
32                Double energySum = energy[seriesCount - 1];
33                Double treshold = energySum * coverage;
34                Int32 effectiveComponents = seriesCount;
35
36                // Determine number of principal component which cover desired part of variance.
37                for (Int32 i = 0; i < seriesCount; ++i)
38                    if (energy[i] >= treshold)
39                    {
40                        effectiveComponents = i;
41                        break;
42                    }
43
44                // Reset number of principal components.
45                pca.TransformedVariablesCount = effectiveComponents;
46
47                // Output results.
48                Console.WriteLine("Transformed Data:");
49                Console.WriteLine(pca.Transform(dataMatrix).ToString("0.000"));
50            }
51            else
52                Console.WriteLine("Error: PCA diverged.");
53        }
54    }
55}

Reference

Other Resources