Least Squares Mutual Information (LSMI)

Mutual information of two continuous random variables X, Y can be defined as:

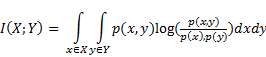
As the calculation of continuous MI by definition on limited statistical data set is impossible due to necessity of knowing exact probability distribution functions, we have to use approximations. The approximation of mutual information between two data series is calculated using Least Squares Mutual Information method. LSMI receives two data series and allows to approximate mutual information between them. The method does not involve density estimation and directly models the density ratio:

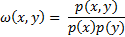
by the following linear model:

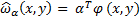
where α = (α₁, α₂, . . . , α_b)^⊤ are parameters to be learned from samples, and φ(x, y) = (φ₁(x, y), φ₂(x, y), . . . , φ_b(x, y))^⊤ are basis functions such that φ(x, y) ≥ 0_b for all (x, y). 0_b denotes the b-dimensional vector with all zeros. b is the basis size of the model. The basis functions φ(x, y):

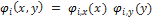
The steps of the algorithm are the following (the input parameters of constructors are marked with bold font):

1. Algorithm randomly chooses basisSize number of centers {c_l | c_l = (u^⊤_l, v^⊤_l)^⊤}^b_l=1 from the input data.

2. Depending on the input series we select one of the cases:

   • In case both series are continuous (useDelta flag should be false): as model candidates, we propose using a Gaussian kernel model:

     

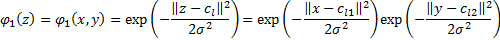
     where sigma will be optimally chosen from the candidates list sigmaList.

   • In case of one series (we consider it is the second one) is discrete φ_i,y should be a Kronecker delta (useDelta flag should be true): Dy,y_i:

     

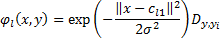
   • If both series are discrete, following approximation doesn’t make any sense, cause in this case mutual information can be found from formula:

     

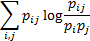
3. In order to estimate model parameter - vector α, we need to maximize Likelihood function under constraint α_i > 0, we obtain the following optimization problem:

   

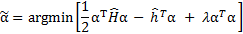
   where lambda is Lagrange multiplier and

   

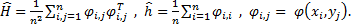
   Differentiating the objective function with respect to α and equating it to zero, we can obtain an analytic-form solution:

   

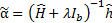
   where I_b is the b-dimensional identity matrix; and the value of lambda will be chosen optimally from the candidates list lambdaList. It will allow us to find solution very fast using Least Squares instead of complex constrained numerical optimization.

4. Algorithm splits all data into basketCount baskets and performs Cross Validation procedure: estimates model parameters on data set with one basket excluded and validates solution fitness on the excluded basket. Model with best CV score will be chosen to calculate final MI value.

Least Squares Mutual Information method is implemented by the LSMI class.

The following constructors create an instance of the class and calculate Mutual Information between series X and Y:

The class provides two methods:

The class provides one property MutualInformation which is the approximation of Mutual Information between two series.

Other Resources