Valuation of Options |
An option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the corresponding obligation to fulfill the transaction.
The price of an option derives from the difference between the reference price and the value of the underlying asset (commonly a stock, a bond, a currency or a futures contract) plus a premium based on the time remaining until the expiration of the option.
This topic contains the following sections:
An option which conveys the right to buy something is called a call; an option which conveys the right to sell is called a put.
The reference price at which the underlying may be traded is called the strike price. The process of activating an option and thereby trading the underlying at the agreed-upon price is referred to as exercising it.
Most options have an expiration date. If the option is not exercised by the expiration date, it becomes void and worthless.
Risk-free rate is the theoretical rate of return of an investment with no risk of financial loss. The risk-free rate represents the interest that an investor would expect from an absolutely risk-free investment over a given period of time.
Annual dividend yield is a financial ratio that shows how much a company pays out in dividends each year relative to its share price. The dividend yield is the return on investment for a stock. Dividend yield is calculated as follows:
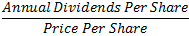
The time to maturity is the time remaining until a financial contract expires. It is measured in years. You have to divide the number of working days remaining to the expiration by the total number of working days per year.
The most common styles of options are American and European. European option – an option that may only be exercised on expiration. American option – an option that may be exercised on any trading day on or before expiry.
Volatility of an option is a variable showing the extent to which the return of the underlying asset will fluctuate between now and the option's expiration. Volatility is derived from the market price of a market traded option.
The Greeks are the quantities representing the sensitivities of the price of the option to a change in underlying parameters on which the value of an instrument or portfolio of financial instruments is dependent. The name is used because the most common of these sensitivities are often denoted by Greek letters. They are also referred to as the risk sensitivities, risk measures or hedge parameters.
The following table shows the relationships between the more common sensitivities to the four primary inputs into a option valuation model and the option's value, delta and gamma. Greeks which are first-order derivatives are in the first row, second-order derivatives are in the second row, and third-order derivatives are in the third row.
For example, Gamma is the derivative of Delta with respect to the underlying instrument's price S, that is why Gamma is on the intersection of Delta row and Stock Price column:
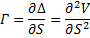
And Gamma is the second-order derivative of the value V of the option with respect to S, that is why Gamma is in the second row of the table.
Stock Price S | Volatility σ | Time To Maturity τ | Risk Free Rate r | |
|---|---|---|---|---|
Value V | Δ Delta | ν Vega | Θ Theta | ρ Rho |
Δ Delta | Γ Gamma | Vanna | Charm | |
Γ Gamma | Speed | Zomma | Color |
For further description see the table of properties in the Basic Implementation section.
Valuation of options is implemented by OptionValuation abstract class. The value of an option can be estimated using a variety of quantitative techniques based on the concept of risk neutral pricing and using stochastic calculus.
The most basic models are:
These models are implemented as child classes which inherit from the parent OptionValuation class.
Option pricing classes have two types of constructors: the regular one and the one involving acceleration. The second constructor requires flags OptionValuationModelOutputs defining the values on which the acceleration is performed. This means the calculation of these values is accelerated. This constructor also requires the number of data sets allowed to be memorized which defines the amount of memory used by the accelerator. The more memory is used the more effective the acceleration is.
Flags OptionValuationModelInputs are used to specify the set of option input parameters.
Implementation of option classes applies the following scheme:
Create an object of class using a constructor. The constructor type depends on what acceleration we want to apply:
no acceleration
with acceleration
with advanced acceleration
Initialization of the created object. Input all the parameters that are required for the calculation.
Get values from properties. Properties and Update methods can be used to update the parameters.
The class provides the following methods, inherited by the child classes:
Method | Description | Performance |
|---|---|---|
set acceleration granularity | Sets acceleration granularity. The less the granularity is, the more time is required for calculation and the more accurate the result is. It is a resource-consuming operation which refreshes the accelerator state. Default value is 1e−5 for the regular acceleration, but it can be greater than this for the advanced acceleration model.
| |
risk free rate | Set risk-free interest rate (e.g. value 0.02 means that yearly risk-free income equals to 2 % of initial money amount if there is no capitalization of interest). It is a resource-consuming operation which refreshes the accelerator state. Get risk-free interest rate. | |
dividends | Set annual dividend yield (e.g. value 0.02 means that yearly dividends income equals to 2 % of the underlying asset stock price). It is a resource-consuming operation which refreshes the accelerator state.
Get annual dividend yield. | |
update option parameters. | Updates option parameters: Update by volatility:
Update by option price:
|
The class provides the following properties, inherited by the child classes:
Property | Description | Performance |
|---|---|---|
stock price | Stock price of the underlying asset. | |
strike price | Strike price of the option. | |
time to maturity | Time to the expiration date. It is measured in years. You have to divide the number of working days remaining to the expiration by the total number of working days per year. | |
option type | Type of option. Can take values:
| |
option style | Option style. Can take values:
| |
value | Value of the option. | |
volatility | Volatility of the underlying asset. | |
delta | Measures the rate of change of option value with respect to changes in the underlying asset's price. Delta is always positive for calls and negative for puts (unless they are zero). 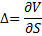 | |
vega | Measures sensitivity to volatility. Vega is the derivative of the option value with respect to the volatility of the underlying asset. 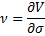 | |
theta | Measures the sensitivity of the value of the derivative to the passage of time: the "time decay." 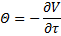 | |
rho | Measures sensitivity to the interest rate: it is the derivative of the option value with respect to the risk free interest rate. 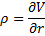 | |
gamma | Measures the rate of change in the delta with respect to changes in the underlying price. All long options have positive gamma and all short options have negative gamma. Gamma is important because it corrects for the convexity of value. 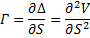 | |
vanna | The sensitivity of the option delta with respect to change in volatility. 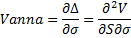 | |
charm | Measures the instantaneous rate of change of delta over the passage of time. 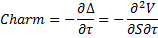 | |
speed | Measures the rate of change in Gamma with respect to changes in the underlying price. 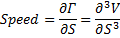 | |
zomma | Measures the rate of change of gamma with respect to changes in volatility. 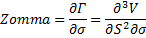 | |
color | Measures the rate of change of gamma over the passage of time. 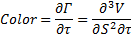 |

