Monte Carlo Model

Monte Carlo model assumes one of the following price models:

• risk neutral geometric Brownian

  

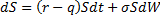
• geometric Brownian

  

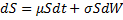
• other (user specified)

  

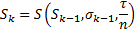
The price of the underlying instrument S is usually modeled such that it follows a geometric Brownian motion with constant drift μ and volatility σ. dW is found via a random sampling from a normal distribution. In a risk neutral model μ = r-q.

The underlying stock price is usually assumed to follow a path that is a function of a Brownian motion or a custom user specified function.

To sample a path following this distribution from time 0 to τ, we chop the time interval into n units of length τ/n, and approximate the Brownian motion or calculate the custom function over the interval τ/n.

In case of Brownian motion the approximation is made by a single normal variable of mean 0 and variance τ/n. The price for a path i = 0..m and time step j = 1..n is found via the following formula:

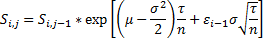
where ε_i is a draw from a standard normal distribution.

To improve the accuracy the antithetic variates method is used which reduces the variance of the sample paths. Due to the antithetic variates method the above formula is applied to the even paths. For the uneven i the following formula is applied:

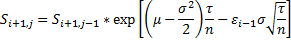
In case of a custom price function the paths are generated according to the formula:

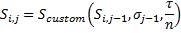
where 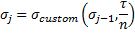is the custom volatility on a particular time step.

The next step is computing the exercise payouts on each step j for each path i.

• European option:

  For call:

  

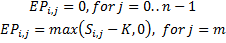
  For put:

  

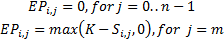
• American option:

  For call:

  

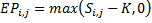
  For put:

  

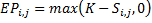
• Custom option:

  

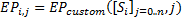
In case of an option that can be executed at a time step before the expiration we have to approximate continuation (non-execution) payoffs. Continuation payoff are computed at each time step, discounted and compared with the execution payout to make a decision whether to execute an option at the particular step or not.

This estimation is done by stepping backward in time. The continuation payoff can be obtained from the simulated path prices via regression. The fitted value from this regression provides a direct estimate of the expected payoff for each exercise time. Comparing it with the value for immediate exercise, the optimal exercise strategy along each path can be estimated well. Discounting back and averaging these values for all paths results in the present value of the option.

This process shall look as follows:

1. Initialize value for each path as the execution payout at the last step:

   

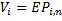
2. Start iterating backwards for each time step j= n-1..0 :

   1. Create a matrix of regression independent variables using the user specified number of basis Laguerre polynomials:

      
      
      

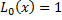
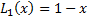
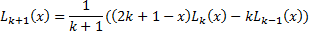
      and set x=stock price at the node. Only those points which have a positive immediate exercise value are picked. Rest of the nodes with 0 or negative payoff are ignored for regression input.

   2. Perform Ordinary Least squares to get coefficients α_k of basis functions.

   3. Compute expected continuation payoff for each path i:

      

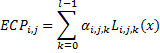
   4. Compare discounted continuation values with the immediate exercise values. If 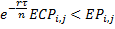, choose to exercise and assign the value for this path equal to the exercise value for the current step:

      

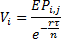
   5. Discount value at each path:

      

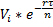
   6. Go to the previous time step until the iterations are done.

3. Calculate expected payoff by averaging. This gives the option value:

   

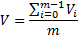
Delegates imply the custom functions computing the price, volatility and exercise payout on each time step. Price and volatility delegates are applied in case of pricing model other than geometric Brownian. Exercise payout delegate is applied in case of custom option type.

The following constructors create an instance of MonteCarlo class with or without usage of performance acceleration.

The following methods initialize the object, set the custom functions and settings and recompute option value.

The class has the following properties that are used to update the source data of the option:

Monte Carlo valuation example:

 1using System;
 2using FinMath.Derivatives;
 3using FinMath.Statistics.Distributions;
 4
 5namespace FinMath.Samples
 6{
 7    class MonteCarloSample
 8    {
 9        static Normal normal = new Normal();
10        static Double riskFreeRate = 0.009;
11
12        static void Main()
13        {
14            Double stockPrice = 350;
15            Double strikePrice = 370;
16            Double annualDividendYield = 0.05;
17            Double timeToMaturity = 1.06;
18            Int32 numberOfSteps = 200;
19            Int32 numberOfPaths = 10000;
20            Int32 numberOfBasisFunctions = 4;
21            Double volatility = 0.22;
22
23            // Initialize MonteCarlo.
24            MonteCarlo monteCarlo = new MonteCarlo();
25            monteCarlo.InitByVolatility(stockPrice, strikePrice, riskFreeRate, annualDividendYield,
26                timeToMaturity, OptionType.Put, OptionStyle.American, numberOfSteps, volatility);
27            monteCarlo.PriceModel = PriceModel.Other;
28            monteCarlo.PricePaths = numberOfPaths;
29            monteCarlo.BasisFunctions = numberOfBasisFunctions;
30            monteCarlo.SetCustomPriceModelFunctions(NextPrice, NextVolatility);
31
32            Console.WriteLine($"Option value = {monteCarlo.Value:0.000}");
33
34            Double stockPrice2 = 352;
35            Double timeToMaturity2 = 1.05;
36
37            // Update asset stock price and time to maturity.
38            monteCarlo.Update(stockPrice2, timeToMaturity2);
39
40            Console.WriteLine($"Option value = {monteCarlo.Value:0.000}");
41
42            // Use another paths of underlying asset price.
43            monteCarlo.RecomputeValue();
44
45            Console.WriteLine($"Option value = {monteCarlo.Value:0.000}");
46        }
47
48        // Custom price model functions.
49        public static Double NextPrice(Double currentPrice, Double currentVolatility, Double timeStep)
50        {
51            return currentPrice * Math.Exp((riskFreeRate - currentVolatility * currentVolatility / 2) * timeStep +
52                currentVolatility * normal.Sample() * Math.Sqrt(timeStep));
53        }
54
55        public static Double NextVolatility(Double currentVolatility, Double timeStep)
56        {
57            return currentVolatility * Math.Exp(normal.Sample() * timeStep);
58        }
59    }
60}

Other Resources