Black-Scholes Model |
The Black–Scholes model is a mathematical model for calculation the price of European-style options.
The Black–Scholes equation is a partial differential equation, which describes the price of the option over time:
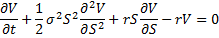
The option price is the analytical solution of this equation.
This topic contains the following sections:
The value of a call option in terms of the Black–Scholes parameters is:
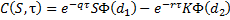
The price of a corresponding put option is:
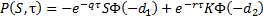
where:
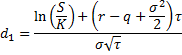
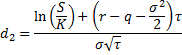
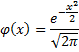 is the standard normal probability density function.
is the standard normal probability density function.
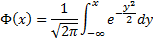 is the standard normal cumulative distribution function.
is the standard normal cumulative distribution function.
S is the stock price of the underlying asset, K is the strike price
r is the risk free rate
q is the annual dividend yield
τ is the time to maturity
σ is the volatility of the underlying asset.
The Greeks for Black–Scholes are given in the table below:
Calls | Puts | |
|---|---|---|
delta | 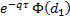 | 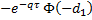 |
theta | 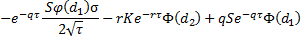 | 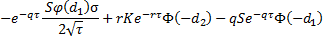 |
gamma | 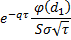 | 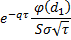 |
vega | 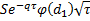 | 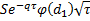 |
rho | 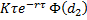 | 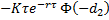 |
vanna | 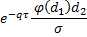 | 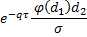 |
charm | 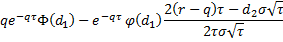 | 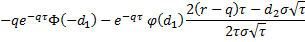 |
speed | 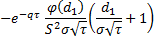 | 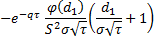 |
zomma | 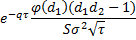 | 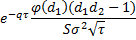 |
color | 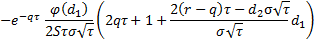 | 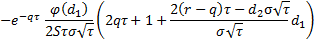 |
The following constructors create an instance of BlackScholes class with or without usage of performance acceleration.
Constructor | Description | Performance |
|---|---|---|
no acceleration | Constructor without parameters for accelerator usage. | |
use acceleration | Constructor that defines which Greeks should be saved for fast recomputation. Note that at each query for any of saveable Greeks all of them will be computed if needed. The parameters passed in to the constructor are: flags for values savable for fast recomputing and maximum number of data sets allowed to be memorized. |
The following methods allow to set acceleration parameters and initialize object with option parameters.
Method | Description | Performance |
|---|---|---|
initialization | Initializes object by option parameters: stock price, strike price, risk free rate, annual dividend yield, time to maturity, option type, volatility or option price.
| |
acceleration settings | Changes acceleration RAM usage. It is a resource-consuming operation which refreshes the accelerator state. |
The class provides static methods for option value and Greeks computation:
Computed Value | Description | Performance |
|---|---|---|
option value | Computes option value.
| |
implied volatility | Computes implied volatility.
| |
delta | Computes the option delta.
| |
theta | Computes the option theta.
| |
gamma | Computes the option gamma. | |
vega | Computes the option vega. | |
rho | Computes the option rho.
| |
vanna | Computes the option vanna. | |
charm | Computes the option charm.
| |
speed | Computes the option speed. | |
zomma | Computes the option zomma. | |
color | Computes the option color. |
Black–Scholes model example:
1using System; 2using FinMath.Derivatives; 3 4namespace FinMath.Samples 5{ 6 class BlackScholesSample 7 { 8 static void Main() 9 { 10 Double stockPrice = 350; 11 Double strikePrice = 370; 12 Double riskFreeRate = 0.009; 13 Double annualDividendYield = 0.05; 14 Double timeToMaturity = 1.06; 15 Double volatility = 0.22; 16 17 BlackScholes blackScholes = new BlackScholes(); 18 19 // Initialize Black-Scholes. 20 blackScholes.InitByVolatility(stockPrice, strikePrice, riskFreeRate, annualDividendYield, 21 timeToMaturity, OptionType.Put, volatility); 22 23 Console.WriteLine($"Value = {blackScholes.Value:0.000}"); 24 Console.WriteLine($"Delta = {blackScholes.Delta:0.000}"); 25 Console.WriteLine($"Theta = {blackScholes.Theta:0.000}"); 26 Console.WriteLine($"Gamma = {blackScholes.Gamma:0.000}"); 27 Console.WriteLine($"Vega = {blackScholes.Vega:0.000}"); 28 Console.WriteLine($"Rho = {blackScholes.Rho:0.000}"); 29 Console.WriteLine(); 30 31 Double stockPrice2 = 352; 32 Double timeToMaturity2 = 1.05; 33 34 // Update asset stock price and time to maturity. 35 blackScholes.Update(stockPrice2, timeToMaturity2); 36 37 Console.WriteLine($"Value = {blackScholes.Value:0.000}"); 38 Console.WriteLine(); 39 40 // Initialize Black-Scholes by option value. 41 BlackScholes blackScholes2 = new BlackScholes(); 42 blackScholes2.InitByOptionPrice(stockPrice2, strikePrice, riskFreeRate, annualDividendYield, 43 timeToMaturity2, OptionType.Put, blackScholes.Value); 44 45 Console.WriteLine($"Implied volatility = {blackScholes2.Volatility:0.000}"); 46 Console.WriteLine($"Delta = {blackScholes2.Delta:0.000}"); 47 Console.WriteLine($"Theta = {blackScholes2.Theta:0.000}"); 48 Console.WriteLine($"Gamma = {blackScholes2.Gamma:0.000}"); 49 Console.WriteLine($"Vega = {blackScholes2.Vega:0.000}"); 50 Console.WriteLine($"Rho = {blackScholes2.Rho:0.000}"); 51 Console.WriteLine(); 52 53 // Use of static methods. 54 Double impliedVolatility = BlackScholes.ImpliedVolatility(stockPrice2, strikePrice, 55 riskFreeRate, annualDividendYield, timeToMaturity2, OptionType.Put, blackScholes.Value); 56 Double delta = BlackScholes.GetDelta(OptionType.Put, stockPrice2, strikePrice, riskFreeRate, 57 annualDividendYield, timeToMaturity2, impliedVolatility); 58 Double theta = BlackScholes.GetTheta(stockPrice2, strikePrice, riskFreeRate, 59 annualDividendYield, timeToMaturity2, OptionType.Put, impliedVolatility); 60 Double gamma = BlackScholes.GetGamma(stockPrice2, strikePrice, riskFreeRate, 61 annualDividendYield, timeToMaturity2, impliedVolatility); 62 Double vega = BlackScholes.GetVega(stockPrice2, strikePrice, riskFreeRate, 63 annualDividendYield, timeToMaturity2, impliedVolatility); 64 Double rho = BlackScholes.GetRho(stockPrice2, strikePrice, riskFreeRate, 65 annualDividendYield, timeToMaturity2, OptionType.Put, impliedVolatility); 66 67 Console.WriteLine($"Implied volatility = {impliedVolatility:0.000}"); 68 Console.WriteLine($"Delta = {delta:0.000}"); 69 Console.WriteLine($"Theta = {theta:0.000}"); 70 Console.WriteLine($"Gamma = {gamma:0.000}"); 71 Console.WriteLine($"Vega = {vega:0.000}"); 72 Console.WriteLine($"Rho = {rho:0.000}"); 73 Console.WriteLine(); 74 75 // Set acceleration settings. 76 BlackScholes blackScholes3 = new BlackScholes(OptionValuation.ModelOutputs.Volatility, 100000); 77 blackScholes3.SetAccelerationGranularity(0.1, 0.1, 0.1, 0.1, 0.1); 78 79 // Use of accelerated version of implied volatility. 80 blackScholes3.InitByOptionPrice(stockPrice2, strikePrice, riskFreeRate, 81 annualDividendYield, timeToMaturity2, OptionType.Put, blackScholes.Value); 82 83 Console.WriteLine($"Implied volatility = {blackScholes3.Volatility:0.000}"); 84 } 85 } 86}

