Binomial Model |
The binomial options pricing model (BOPM) provides a generalizable numerical method for the valuation of options. Essentially, the model uses a “discrete-time” (lattice based) model of the varying price over time of the underlying financial instrument.
This topic contains the following sections:
The binomial pricing model traces the evolution of the option's key underlying variables in discrete-time. This is done by means of a binomial lattice, for a number of time steps between the valuation and expiration dates. Each node in the lattice represents a possible price of the underlying at a given point in time.
Valuation is performed iteratively, starting at each of the final nodes (those that may be reached at the time of expiration), and then working backwards through the tree towards the first node (valuation date). The value computed at each stage is the value of the option at that point in time.
Option valuation using this method is, as described, a three-step process:
price tree generation
calculation of option value at each final node
sequential calculation of the option value at each preceding node
Step 1: Create the binomial price tree
At each step, it is assumed that the underlying instrument will move up or down by a specific factor (u or d) per step of the tree (where, by definition, u>1 and 0<d<1). The up and down factors are calculated using the underlying volatility, σ, and the time duration of a step, t, measured in years (using the day count convention of the underlying instrument). So, if S is the current price, the next price will be:
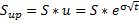
or
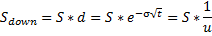
The tree is recombinant, i.e. if the underlying asset moves up and then down (u,d), the price will be the same as if it had moved down and then up (d,u) — here the two paths merge or recombine. This property reduces the number of tree nodes, and thus accelerates the computation of the option price.
This property also allows that the value of the underlying asset at each node can be calculated directly via formula, and does not require that the tree be built first. The node-value will be:
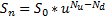
Step 2: Find option value at each final node
At each final node of the tree — i.e. at expiration of the option — the option value is simply its intrinsic, or exercise, value.
Max [ (Sn − K), 0 ], for a call option
Max [ (K – Sn), 0 ], for a put option.
Where K is the strike price and Sn is the stock price of the underlying asset at the n-th period.
Step 3: Find option value at earlier nodes
The following formula to compute the option value is applied at each node:
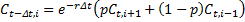
Ct,i is the option's value for the i-th node at time t,
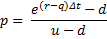 - "probability" p of an up move in the underlying, and "probability" (1-p) of a down move.
- "probability" p of an up move in the underlying, and "probability" (1-p) of a down move.
r is the risk free rate, q is the annual dividend yield.
For a European option, there is no option of early exercise, and the binomial value applies at all nodes. For an American option, since the option may either be held or exercised prior to expiry, the value at each node is: Max (Binomial Value, Exercise Value).
In reality option market makers prefer to specify dividends in terms of a fixed cash value instead of a percentage. Standard approximation schemes can no longer be applied, or it becomes extremely inefficient from a computational point of view to do so. As a result, certain approximations have been proposed in the Vellekoop method to find option prices when the underlying asset pays cash dividends in the future:
Build a binomial tree with n time steps as usual. At the end of the tree we can now calculate the value of option for all final nodes. We now work backwards through the binomial tree as usual until we arrive at a dividend date (i.e. to timestep m(n)). The result of having worked backwards through the tree is the set of (approximate) values fn(s) for the option contract in all the points s of the binomial tree at timestep m(n). These values fn(s) approximate the option values at a time just after the dividend has been paid, given that the stock price at that time equals s.
To be able to continue backwards through the tree we now have to find the option values just before the dividend is paid. Since the stock price jumps down with an amount D when it goes ex-dividend, the option value for a stock price s just before the dividend date equals the option value for a stock price s-D just after the dividend date. We thus need the option values fn in all the points s-D of the binomial tree at timestep m(n), but we have only calculated the values of fn(s) at timestep m(n). We therefore define a function which approximates the function fn on the whole
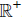 ,
based on the values of fn on timestep m(n). This interpolating
function is denoted by
,
based on the values of fn on timestep m(n). This interpolating
function is denoted by 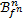 ,
and we can then calculate the values
,
and we can then calculate the values 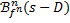 as approximations
for the values of fn(s-D) on timestep m(n), which we need to
continue the binomial method in the point s.
as approximations
for the values of fn(s-D) on timestep m(n), which we need to
continue the binomial method in the point s.After that we work further backwards through the tree, until we reach time zero, and the option value has been found.
The extension of this method to more than one dividend is obvious.
The following constructors create an instance of Binomial class with or without usage of performance acceleration.
Constructor | Description | Performance |
|---|---|---|
no acceleration | Constructor without parameters for accelerator usage. | |
use acceleration | Constructor that defines which Greeks should be saved for fast recomputation. Note that at each query for any of saveable Greeks all of them will be computed if needed. The parameters passed in to the constructor are: flags for values savable for fast recomputing and maximum number of data sets allowed to be memorized. | |
use advanced acceleration | Enables advanced acceleration mode for specified option properties. Allowed properties for advanced acceleration are: OptionValue, Volatility, Delta. The parameters passed into the constructor are: flags for arguments that may be changed significantly, flags for properties with advanced acceleration and maximum number of data sets allowed to be memorized.
|
The class provides the following methods:
Method | Description | Performance |
|---|---|---|
initialization | Initializes object by option parameters: stock price, strike price, risk free rate, annual dividend yield, time to maturity, option type, option style, steps, volatility or option price.
Initializes object by option parameters. For option with discrete dividends. The dividends should be specified using the structure Dividend
| |
compute option value | Computes option value.
Computes option value for underlying asset price with discrete dividends using Vellekoop method.
| |
compute implied volatility | Computes the underlying asset implied volatility.
For option with discrete dividends: | |
set precision | Option value for asset with volatility equal to ImpliedVolatility return should be in [OptionValue∙(1 − precision), OptionValue∙(1 + precision)]. Default value is 1e-7. It is a resource-consuming operation which refreshes the accelerator state. | |
dividends | Returns copy of actual underlying asset discrete dividends list. Sets new list of the underlying asset discrete dividends. It is a resource-consuming operation which refreshes the accelerator state. |
The class provides the following property:
Property | Description | Performance |
|---|---|---|
number of steps | Sets the number of steps in binomial model |
Binomial model example:
1using System; 2using FinMath.Derivatives; 3 4namespace FinMath.Samples 5{ 6 class BinomialSample 7 { 8 static void Main() 9 { 10 Double stockPrice = 350; 11 Double strikePrice = 370; 12 Double riskFreeRate = 0.009; 13 Double annualDividendYield = 0.05; 14 Double timeToMaturity = 1.06; 15 Int32 numberOfSteps = 200; 16 Double volatility = 0.22; 17 18 // Use of static methods for option value computation. 19 Double optionValue = Binomial.OptionValue(stockPrice, strikePrice, riskFreeRate, annualDividendYield, 20 timeToMaturity, OptionType.Put, OptionStyle.American, numberOfSteps, volatility); 21 22 Console.WriteLine($"Option value = {optionValue:0.000}"); 23 24 // Use of static methods for implied volatility computation. 25 Double impliedVolatility = Binomial.ImpliedVolatility(stockPrice, strikePrice, riskFreeRate, 26 annualDividendYield, timeToMaturity, OptionType.Put, OptionStyle.American, numberOfSteps, optionValue); 27 28 Console.WriteLine($"Implied volatility = {impliedVolatility:0.000}"); 29 Console.WriteLine(); 30 31 // Create new Binomial instance. 32 Binomial binomial = new Binomial(); 33 34 // Discrete dividends usage sample. 35 Dividend[] dividens = new Dividend[4]; 36 dividens[0].timeToPayment = 0.355; 37 dividens[0].dividendsAmount = 3.45; 38 39 dividens[1].timeToPayment = 1.055; 40 dividens[1].dividendsAmount = 4.45; 41 42 // Order of elements in list is inessential. 43 dividens[2].timeToPayment = 0.755; 44 dividens[2].dividendsAmount = 5.45; 45 46 // Dividends paid in the past or after option expiration are ignored. 47 dividens[3].timeToPayment = -0.045; 48 dividens[3].dividendsAmount = 3.45; 49 50 // Set option parameters. 51 binomial.InitByVolatility(stockPrice, strikePrice, riskFreeRate, dividens, 52 timeToMaturity, OptionType.Put, OptionStyle.American, numberOfSteps, volatility); 53 54 Console.WriteLine($"Option value = {binomial.Value:0.000}"); 55 Console.WriteLine($"Delta = {binomial.Delta:0.000}"); 56 57 Double stockPrice2 = 352; 58 Double timeToMaturity2 = 1.05; 59 60 // Update asset stock price and time to maturity. 61 binomial.Update(stockPrice2, timeToMaturity2); 62 63 Console.WriteLine($"Option value = {binomial.Value:0.000}"); 64 Console.WriteLine($"Delta = {binomial.Delta:0.000}"); 65 66 // Initialize Binomial by option value. 67 Binomial binomialByValue = new Binomial(); 68 binomialByValue.InitByOptionPrice(stockPrice2, strikePrice, riskFreeRate, dividens, 69 timeToMaturity2, OptionType.Put, OptionStyle.American, numberOfSteps, binomial.Value); 70 71 Console.WriteLine($"Implied volatility = {binomialByValue.Volatility:0.000}"); 72 Console.WriteLine($"Delta = {binomialByValue.Delta:0.000}"); 73 Console.WriteLine(); 74 75 // Use of accelerated computation. 76 binomial = new Binomial(OptionValuation.ModelOutputs.OptionValue | OptionValuation.ModelOutputs.Delta, 100000); 77 78 // Change acceleration granularity. 79 binomial.SetAccelerationGranularity(0.001, 0.001, 0.001, 0.001, 0.001); 80 81 // Initialize. 82 binomial.InitByVolatility(stockPrice, strikePrice, riskFreeRate, annualDividendYield, 83 timeToMaturity, OptionType.Put, OptionStyle.American, numberOfSteps, volatility); 84 85 // Use of accelerated version of option valuation. 86 Console.WriteLine($"Option value = {binomial.Value:0.000}"); 87 Console.WriteLine($"Delta = {binomial.Delta:0.000}"); 88 89 // Enable implied volatility and delta computation acceleration. 90 binomialByValue = new Binomial(OptionValuation.ModelOutputs.Volatility | OptionValuation.ModelOutputs.Delta, 100000); 91 92 // Change acceleration granularity. 93 binomialByValue.SetAccelerationGranularity(0.001, 0.001, 0.001, 0.001, 0.001); 94 95 // Initialize. 96 binomialByValue.InitByOptionPrice(stockPrice, strikePrice, riskFreeRate, annualDividendYield, 97 timeToMaturity, OptionType.Put, OptionStyle.American, numberOfSteps, optionValue); 98 99 // Use of accelerated version of implied volatility and delta valuation. 100 Console.WriteLine($"Implied volatility = {binomialByValue.Volatility:0.000}"); 101 Console.WriteLine($"Delta = {binomialByValue.Delta:0.000}"); 102 Console.WriteLine(); 103 104 // Use of advanced acceleration. 105 binomial = new Binomial( 106 OptionValuation.ModelInputs.StockPrice | OptionValuation.ModelInputs.StrikePrice | OptionValuation.ModelInputs.Volatility, 107 OptionValuation.ModelOutputs.OptionValue | OptionValuation.ModelOutputs.Delta, 100000); 108 109 binomial.SetAccelerationGranularity(0.1, 0.1, 0.001, 0.1, 0.1); 110 binomial.InitByVolatility(stockPrice, strikePrice, riskFreeRate, annualDividendYield, 111 timeToMaturity, OptionType.Put, OptionStyle.American, numberOfSteps, volatility); 112 Console.WriteLine($"Option value = {binomial.Value:0.000}"); 113 Console.WriteLine($"Delta = {binomial.Delta:0.000}"); 114 115 binomialByValue = new Binomial( 116 OptionValuation.ModelInputs.StockPrice | OptionValuation.ModelInputs.StrikePrice | OptionValuation.ModelInputs.OptionPrice, 117 OptionValuation.ModelOutputs.Volatility | OptionValuation.ModelOutputs.Delta, 100000); 118 binomial.SetAccelerationGranularity(0.1, 0.1, 0.001, 0.1, 0.1); 119 binomialByValue.InitByOptionPrice(stockPrice, strikePrice, riskFreeRate, annualDividendYield, 120 timeToMaturity, OptionType.Put, OptionStyle.American, numberOfSteps, optionValue); 121 Console.WriteLine($"Implied volatility = {binomialByValue.Volatility:0.000}"); 122 Console.WriteLine($"Delta = {binomialByValue.Delta:0.000}"); 123 Console.WriteLine(); 124 } 125 } 126}


