LU Decomposition |
In linear algebra LU decomposition is a decomposition of real square matrix into the product of a lower triangular matrix and upper triangular matrix. This decomposition is used to solve systems of linear equations or calculate the determinant of a matrix.
This topic contains the following sections:
StatementAny real square matrix A may be decomposed as:
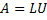
where L is a lower triangular matrix with unit diagonal elements and U is an upper triangular matrix:
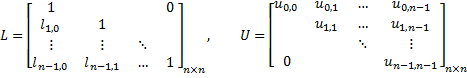
The product sometimes includes a permutation matrix as well, i.e. a matrix of zeros and ones that has exactly one entry 1 in each row and column:
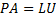
ConstructorsConstructors initialize a new instance of LU factorization of the given matrix.
Constructor | Description | Performance |
|---|---|---|
create new instance of LU decomposition | ||
pass the data matrix | User specifies a matrix to factorize as a parameter. |
Basic methodsThis method group includes getting decomposition matrices, updating data matrix and calculating permutation.
Operation | Description | Performance |
|---|---|---|
update data matrix | Computes the LU factorization of the given matrix. | |
L matrix | Returns the lower triangular matrix L with unit diagonal elements. | |
U matrix | Returns the upper triangular matrix U. | |
permutation matrix | Computes the permutation matrix. | |
permutation | Computes the permutation of rows applied to matrix A (permutation is an integer array). | |
inversed permutation | Computes the inversed permutation of rows applied to matrix A (inversed permutation is an integer array). | |
determinant | Returns the determinant of the matrix. | |
is singular | Returns the boolean flag that indicates whether the matrix is singular. |
ApplicationsThis method group includes calculating inverse matrix and solving system of linear equations.
Operation | Description | Performance |
|---|---|---|
inverse matrix | Computes the inverse matrix. Returning result:Out of place: | |
solve system of matrix equations | Solves a system of linear equations AX = B, where A is our data matrix and B and X are matrices. Returning result:Out of place: | |
solve system of linear equations | Solves a system of linear equations Ax = b, where A is our data matrix and b and x are vectors. Returning result:Out of place: |
Code SampleThe example of LU class usage:
1using System; 2using FinMath.LinearAlgebra; 3using FinMath.LinearAlgebra.Factorizations; 4 5namespace FinMath.Samples 6{ 7 class LUFactorization 8 { 9 static void Main() 10 { 11 // Generate random positive definite matrix. 12 Matrix A = Matrix.Random(4, 4); 13 Console.WriteLine(A.ToString("0.000")); 14 Console.WriteLine(); 15 16 // Create an instance of Cholesky factorization. 17 LU lu = new LU(A); 18 19 // Print lower factor. 20 Console.WriteLine(lu.L().ToString("0.000")); 21 Console.WriteLine(); 22 23 // Print upper factor. 24 Console.WriteLine(lu.U().ToString("0.000")); 25 Console.WriteLine(); 26 27 // Print determinant. 28 Console.WriteLine($"Determinant = {lu.Determinant():0.000}"); 29 Console.WriteLine(); 30 31 // Generate random right-hand side. 32 Vector B = Vector.Random(4); 33 Console.WriteLine($"B = {B.ToString("0.000")}"); 34 35 // Solve system A * X = B using already built Cholesky factorization. 36 Vector X = lu.Solve(B); 37 Console.WriteLine($"X = {X.ToString("0.000")}"); 38 39 // Print norm of error. 40 Console.WriteLine(); 41 Console.WriteLine($"Error = {(B - A * X).L2Norm():E8}"); 42 } 43 } 44}
See Also