SVD Decomposition

In linear algebra the singular value decomposition (SVD) is a decomposition of a real m×n matrix into the product of an m×m unitary matrix U, m×n diagonal matrix S with nonnegative real numbers on the main diagonal and transpose of n×n unitary matrix V.

This topic contains the following sections:

Statement
Constructors
Basic methods
Applications
Code Sample
See Also

Statement

Any m×n real matrix A may be decomposed as:

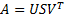
where U is an m×m unitary matrix, S is an m×n diagonal matrix with nonnegative real numbers on the diagonal, and V is an n×n unitary matrix.

The diagonal entries of S are known as the singular values of A.

The columns of U and V are, respectively, left- and right-singular vectors for the corresponding singular values.

The following types of SVD decomposition are available:

Full SVD
Singular values and all singular vectors are calculated.
In applications it is quite unusual for the full SVD to be required. Instead, it is often sufficient (as well as faster, and more economical for storage) to compute a reduced version of the SVD.
Thin SVD
Only the min(m,n) column vectors of U corresponding to the row vectors of transpose of V are calculated. The remaining column vectors of U are not calculated. This is significantly quicker and more economical than the full SVD if n<<m.
None SVD
Only the singular values of A are calculated. Singular vectors are not calculated.

Constructors

Constructors initialize a new instance of SVD factorization of the given matrix.

Constructor	Description	Performance
pass the data matrix	User specifies a matrix to factorize as a parameter. SVD(Matrix)
specify the singular vectors to compute	User specifies left and right singular vectors he is interested in. SVD(SVDVectorSet, SVDVectorSet)
specify the matrix and the singular vectors to compute	SVD(Matrix, SVDVectorSet, SVDVectorSet)
NoneSVD	User specifies the data matrix for the NoneSVD decomposition. NoneSVD(Matrix)
ThinSVD	User specifies the data matrix for the ThinSVD decomposition. ThinSVD(Matrix)
FullSVD	User specifies the data matrix for the FullSVD decomposition. FullSVD(Matrix)

Basic methods

This method group includes getting decomposition matrices, updating data matrix and calculating permutation.

Operation	Description	Performance
update data matrix	Computes the SVD factorization of the given matrix. Update(Matrix)
singular values	Returns the vector whose element are singular values (in decreasing order). S
U matrix	Returns the matrix whos columns are left singular vectors we are interested in. U
VT matrix	Returns the matrix whos rows are right singular vectors we are interested in. VT
condition number	Returns the condition number of the matrix in L2-norm (Euclidean norm). ConditionNumber
L2 (Euclidean) norm	Returns the L2-norm of the matrix. L2Norm
rank	Returns the rank of the matrix. Rank
reciprocals of singular values	Computes the vector of reciprocals of singular values taking into account possible roundoff errors. SPlus
is converged	Returns whether the SVD algorithm converged or not. IsConverged

Applications

This method group includes solving system of linear equations.

Operation	Description	Performance
solve system of matrix equations	Solves a system of linear equations AX = B, where A is our data matrix and B and X are matrices. Returning result: Solve(Matrix) Out of place: Solve(Matrix, Matrix)
solve system of linear equations	Solves a system of linear equations Ax = b, where A is our data matrix and b and x are vectors. Returning result: Solve(Vector) Out of place: Solve(Vector, Vector)

Operation

Description

Performance

solve system of matrix equations

Solves a system of linear equations AX = B, where A is our data matrix and B and X are matrices.

Returning result:

method Solve(Matrix)

Out of place:

method Solve(Matrix, Matrix)

solve system of linear equations

Solves a system of linear equations Ax = b, where A is our data matrix and b and x are vectors.

Returning result:

method Solve(Vector)

Out of place:

method Solve(Vector, Vector)

Code Sample

The example of SVD class usage:

Copy

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.LinearAlgebra.Factorizations;
 4
 5namespace FinMath.Samples
 6{
 7    class SingularValueDecomposition
 8    {
 9        static void Main()
10        {
11            // Generate random matrix.
12            Matrix A = Matrix.Random(3, 4);
13            Console.WriteLine("A = ");
14            Console.WriteLine(A.ToString("0.000"));
15            Console.WriteLine();
16
17            // Perform factorization. We are going to compute all left and write
18            // singular vectors.
19            SVD svd = new SVD(A, SVD.VectorSet.Full, SVD.VectorSet.Full);
20
21            // Print singular values.
22            Console.WriteLine($"Singular Values = {svd.S().ToString("0.000")}");
23            Console.WriteLine();
24
25            // Print left singular vectors.
26            Console.WriteLine("U = ");
27            Console.WriteLine(svd.U().ToString("0.000"));
28            Console.WriteLine();
29
30            // Print numerical rank.
31            Console.WriteLine($"Rank = {svd.Rank()}");
32            Console.WriteLine();
33
34            // Print L2 norm.
35            Console.WriteLine($"L2 Norm = {svd.L2Norm()}");
36            Console.WriteLine();
37
38            // Print condition number.
39            Console.WriteLine($"Condition Number = {svd.ConditionNumber()}");
40            Console.WriteLine();
41        }
42    }
43}

Other Resources

Factorizations

Cholesky Decomposition

LQ Decomposition

LU Decomposition

QR Decomposition