Click or drag to resize

QR Decomposition

In linear algebra QR decomposition is a decomposition of real matrix into the product of a unitary matrix Q and upper triangular (or upper trapezoidal) matrix R.

This topic contains the following sections:

Statement

Any real matrix A may be decomposed as:

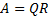
FDecompQR

where R is an upper triangular (or upper trapezoidal) matrix and Q is a unitary matrix:

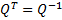
FUnitary

QR decomposition with column pivoting introduces a permutation matrix P:

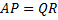
FColumn Pivoting

Column pivoting is useful when A is (nearly) rank deficient, or is suspected of being so. It can also improve numerical accuracy.

Constructors

Constructors initialize a new instance of QR factorization of the given matrix.

Constructor

Description

Performance

pass the data matrix

User specifies a matrix to factorize as a parameter.

methodQR(Matrix)

use column pivoting

The boolean flag indicates whether to use column pivoting or not.

methodQR(Boolean)

In case of this constructor data matrix is unspecified, therefore user needs to use Update(Matrix data) method after initializing the factorization instance to set the matrix to factorize.

use column pivoting and set data matrix

The boolean flag indicates whether to use column pivoting or not.

methodQR(Matrix, Boolean)

Basic methods

This method group includes getting decomposition matrices, updating data matrix and calculating permutation.

Operation

Description

Performance

update data matrix

Computes the QR factorization of the given matrix.

methodUpdate(Matrix)

R matrix

Returns the upper triangular (upper trapezoidal) matrix R.

methodR

Q matrix

Returns the unitary matrix Q.

methodQ

economy-size R matrix

Returns the economy-size upper triangular matrix L.

For example if we have QR decomposition like the following: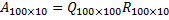

FDecomp EconomyQR

Thus matrix R is upper trapezoidal we can remove the lower 90 zero rows from matrix R and remove 90 columns from matrix Q. Such decomposition remains valid, but matrix Q will be no longer unitary, only it's columns will be orthogonal: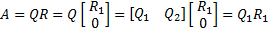

FDecomp EconomyQR 1

methodEconomicR

economy-size Q matrix

Computes the economy-size matrix Q with orthogonal columns (see the description above).

methodEconomicQ

permutation matrix

Computes the permutation matrix.

methodP

permutation

Computes the permutation of columns applied to matrix A (it is an integer array).

methodColumnPermutation

inversed permutation

Computes the inversed permutation of columns applied to matrix A (it is an integer array).

methodInverseColumnPermutation

is full rank

Checks whether the matrix has full rank.

methodIsFullRank

Applications

This method group includes solving system of linear equations.

Operation

Description

Performance

solve system of matrix equations

Solves a system of linear equations AX = B, where A is our data matrix and B and X are matrices.

Returning result:

methodSolve(Matrix)

Out of place:

methodSolve(Matrix, Matrix)

solve system of linear equations

Solves a system of linear equations Ax = b, where A is our data matrix and b and x are vectors.

Returning result:

methodSolve(Vector)

Out of place:

methodSolve(Vector, Vector)

Code Sample

The example of QR class usage:

C#
Copy
 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.LinearAlgebra.Factorizations;
 4
 5namespace FinMath.Samples
 6{
 7    class QRFactorization
 8    {
 9        static void Main()
10        {
11            // Generate random rectangular matrix.
12            Matrix A = Matrix.Random(4, 2);
13            Console.WriteLine("A = ");
14            Console.WriteLine(A.ToString("0.000"));
15            Console.WriteLine();
16
17            // Perform QR factorization.
18            QR qr = new QR(A, false);
19
20            // Print matrix Q.
21            Console.WriteLine("Q = ");
22            Console.WriteLine(qr.Q().ToString("0.000"));
23            Console.WriteLine();
24
25            // Print matrix R.
26            Console.WriteLine("R = ");
27            Console.WriteLine(qr.R().ToString("0.000"));
28            Console.WriteLine();
29
30            // Disperancy of factorization.
31            Console.WriteLine($"Norm(A - Q * R) = {(A - qr.Q() * qr.R()).L2Norm():E8}");
32            Console.WriteLine();
33
34            // Print economic matrix Q.
35            Console.WriteLine("Economic Q = ");
36            Console.WriteLine(qr.EconomicQ().ToString("0.000"));
37            Console.WriteLine();
38
39            // Print economic matrix R.
40            Console.WriteLine("Economic R = ");
41            Console.WriteLine(qr.EconomicR().ToString("0.000"));
42            Console.WriteLine();
43
44            // Disperancy of economic factorization.
45            Console.WriteLine($"Norm(A - Q * R) = {(A - qr.EconomicQ() * qr.EconomicR()).L2Norm():E8}");
46            Console.WriteLine();
47
48            // Generate overdetermined system of linear equation and solve it.
49            Vector B = A * Vector.Random(2);
50            Vector X = qr.Solve(B);
51
52            // Print found solution.
53            Console.WriteLine("X = ");
54            Console.WriteLine(X.ToString("0.000"));
55            Console.WriteLine();
56
57            // Print error.
58            Console.WriteLine($"Error = {(B - A * X).L2Norm():E8}");
59        }
60    }
61}

See Also