Cholesky Decomposition

In linear algebra Cholesky decomposition (or Cholesky triangle) is a decomposition of real square positive-definite matrix into the product of a lower triangular matrix and its transpose. It was discovered by André-Louis Cholesky for real matrices and is an example of a square root of a matrix. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations.

This topic contains the following sections:

Statement
Constructors
Basic methods
Applications
Code Sample
See Also

Statement

If matrix A is real square and positive definite, then A can be decomposed as:

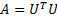
where U is an upper triangular matrix with strictly positive diagonal entries, or:

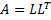
where L is a lower triangular matrix with strictly positive diagonal entries.

The Cholesky decomposition is unique.

Constructors

Constructors initialize a new instance of Cholesky factorization of the given matrix.

Constructor	Description	Performance
pass the data matrix	User specifies a matrix to factorize as a parameter. Cholesky(Matrix)
indicate form of the Cholesky factorization	true indicates factorization in the form: A = U'U, where U is upper triangular matrix. false indicates factorization in the form: A = LL', where L is lower triangular matrix. Whatever form of Cholesky factorization you choose you still will be able to get both upper and lower Cholesky factors. Cholesky(Boolean) In case of this constructor data matrix is unspecified, therefore user needs to use Update(Matrix data) method after initializing the factorization instance to set the matrix to factorize.
indicate form of the Cholesky factorization and set data matrix	true indicates factorization in the form: A = U'U, where U is upper triangular matrix. false indicates factorization in the form: A = LL', where L is lower triangular matrix. Whatever form of Cholesky factorization you choose you still will be able to get both upper and lower Cholesky factors. Cholesky(Matrix, Boolean)

Constructor

Description

Performance

pass the data matrix

User specifies a matrix to factorize as a parameter.

method Cholesky(Matrix)

indicate form of the Cholesky factorization

true indicates factorization in the form: A = U'U, where U is upper triangular matrix.

false indicates factorization in the form: A = LL', where L is lower triangular matrix.

Whatever form of Cholesky factorization you choose you still will be able to get both upper and lower Cholesky factors.

method Cholesky(Boolean)

In case of this constructor data matrix is unspecified, therefore user needs to use Update(Matrix data) method after initializing the factorization instance to set the matrix to factorize.

indicate form of the Cholesky factorization and set data matrix

true indicates factorization in the form: A = U'U, where U is upper triangular matrix.

false indicates factorization in the form: A = LL', where L is lower triangular matrix.

Whatever form of Cholesky factorization you choose you still will be able to get both upper and lower Cholesky factors.

method Cholesky(Matrix, Boolean)

Basic methods

This method group includes getting decomposition triangular matrices, updating data matrix and calculating determinant.

Operation	Description	Performance
is positive definite	Returns "true" in case matrix is positive definite (it also indicates that Cholesky factorization has been built). IsPositiveDefinite
update data matrix	Computes Cholesky factorization of the given matrix. Update(Matrix)
L / U matrices	Return the lower/upper Cholesky factor. It is a lower/upper triangular matrix with positive diagonal elements. L U
determinant	Returns the determinant of the matrix. Determinant

Applications

This method group includes calculating inverse matrix and solving system of linear equations.

Operation	Description	Performance
inverse matrix	Computes the inverse matrix. Returning result: GetInverse Out of place: GetInverse
solve system of matrix equations	Solves a system of linear equations AX = B, where A is our data matrix and B and X are matrices. Returning result: Solve(Matrix) Out of place: Solve(Matrix, Matrix)
solve system of linear equations	Solves a system of linear equations Ax = b, where A is our data matrix and b and x are vectors. Returning result: Solve(Vector) Out of place: Solve(Vector, Vector)

Operation

Description

Performance

inverse matrix

Computes the inverse matrix.

solve system of matrix equations

Solves a system of linear equations AX = B, where A is our data matrix and B and X are matrices.

Returning result:

method Solve(Matrix)

Out of place:

method Solve(Matrix, Matrix)

solve system of linear equations

Solves a system of linear equations Ax = b, where A is our data matrix and b and x are vectors.

Returning result:

method Solve(Vector)

Out of place:

method Solve(Vector, Vector)

Code Sample

The example of Cholesky class usage:

Copy

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.LinearAlgebra.Factorizations;
 4
 5namespace FinMath.Samples
 6{
 7    class CholeskyFactorization
 8    {
 9        static void Main()
10        {
11            // Generate random positive definite matrix.
12            Matrix M = Matrix.Random(4, 4);
13            Matrix A = M * M.GetTransposed();
14            Console.WriteLine(A.ToString("0.000"));
15            Console.WriteLine();
16
17            // Create an instance of Cholesky factorization.
18            Cholesky cholesky = new Cholesky(A, false);
19
20            // Print lower Cholesky factor.
21            Console.WriteLine(cholesky.L().ToString("0.000"));
22            Console.WriteLine();
23
24            // Print determinant.
25            Console.WriteLine($"Determinant = {cholesky.Determinant():0.000}");
26            Console.WriteLine();
27
28            // Generate random right-hand side.
29            Vector B = Vector.Random(4);
30            Console.WriteLine($"B = {B.ToString("0.000")}");
31
32            // Solve system A * X = B using already built Cholesky factorization.
33            Vector X = cholesky.Solve(B);
34            Console.WriteLine($"X = {X.ToString("0.000")}");
35
36            // Print norm of error.
37            Console.WriteLine();
38            Console.WriteLine($"Error = {(B - A * X).L2Norm():E8}");
39        }
40    }
41}

Other Resources