Click or drag to resize

LQ Decomposition

In linear algebra LQ decomposition is a decomposition of real matrix into the product of a lower triangular (or lower trapezoidal) matrix and unitary matrix.

This topic contains the following sections:

Statement

Any real matrix A may be decomposed as:

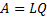
FDecompLQ

where L is a lower triangular (or lower trapezoidal) matrix and Q is a unitary matrix:

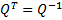
FUnitary

LQ decomposition with row pivoting introduces a permutation matrix P:

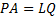
FRow Pivoting

Row pivoting is useful when A is (nearly) rank deficient, or is suspected of being so. It can also improve numerical accuracy.

Constructors

Constructors initialize a new instance of LQ factorization of the given matrix.

Constructor

Description

Performance

pass the data matrix

User specifies a matrix to factorize as a parameter.

methodLQ(Matrix)

use row pivoting

The boolean flag indicates whether to use row pivoting or not.

methodLQ(Boolean)

In case of this constructor data matrix is unspecified, therefore user needs to use Update(Matrix data) method after initializing the factorization instance to set the matrix to factorize.

use row pivoting and set data matrix

The boolean flag indicates whether to use row pivoting or not.

methodLQ(Matrix, Boolean)

Basic methods

This method group includes getting decomposition matrices, updating data matrix and calculating permutation.

Operation

Description

Performance

update data matrix

Computes the LQ factorization of the given matrix.

methodUpdate(Matrix)

L matrix

Returns the lower triangular (lower trapezoidal) matrix L.

methodL

Q matrix

Returns the unitary matrix Q.

methodQ

economy-size L matrix

Returns the economy-size lower triangular matrix L.

For example if we have LQ decomposition like the following: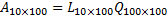

FDecomp EconomyLQ

Thus matrix L is lower trapezoidal we can remove the right 90 zero columns from matrix L and remove 90 rows from matrix Q. Such decomposition remains valid, but matrix Q will be no longer unitary, only it's rows will be orthogonal: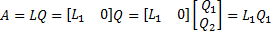

FDecomp EconomyLQ 1

methodEconomicL

economy-size Q matrix

Computes the economy-size matrix Q with orthogonal rows (see the description above).

methodEconomicQ

permutation matrix

Computes the permutation matrix.

methodP

permutation

Computes the permutation of rows applied to matrix A (it is an integer array).

methodRowPermutation

inversed permutation

Computes the inversed permutation of rows applied to matrix A (it is an integer array).

methodInverseRowPermutation

is full rank

Checks whether the matrix has full rank.

methodIsFullRank

Applications

This method group includes solving system of linear equations.

Operation

Description

Performance

solve system of matrix equations

Solves a system of linear equations AX = B, where A is our data matrix and B and X are matrices.

Returning result:

methodSolve(Matrix)

Out of place:

methodSolve(Matrix, Matrix)

solve system of linear equations

Solves a system of linear equations Ax = b, where A is our data matrix and b and x are vectors.

Returning result:

methodSolve(Vector)

Out of place:

methodSolve(Vector, Vector)

Code Sample

The example of LQ class usage:

C#
Copy
 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.LinearAlgebra.Factorizations;
 4
 5namespace FinMath.Samples
 6{
 7    class LQFactorization
 8    {
 9        static void Main()
10        {
11            // Generate random rectangular matrix.
12            Matrix A = Matrix.Random(2, 4);
13            Console.WriteLine("A = ");
14            Console.WriteLine(A.ToString("0.000"));
15            Console.WriteLine();
16
17            // Perform LQ factorization.
18            LQ lq = new LQ(A, false);
19
20            // Print matrix L.
21            Console.WriteLine("L = ");
22            Console.WriteLine(lq.L().ToString("0.000"));
23            Console.WriteLine();
24
25            // Print matrix Q.
26            Console.WriteLine("Q = ");
27            Console.WriteLine(lq.Q().ToString("0.000"));
28            Console.WriteLine();
29
30            // Disperancy of factorization.
31            Console.WriteLine($"Norm(A - L * Q) = {(A - lq.L() * lq.Q()).L2Norm():E8}");
32            Console.WriteLine();
33
34            // Print economic matrix L.
35            Console.WriteLine("Economic L = ");
36            Console.WriteLine(lq.EconomicL().ToString("0.000"));
37            Console.WriteLine();
38
39            // Print economic matrix Q.
40            Console.WriteLine("Economic Q = ");
41            Console.WriteLine(lq.EconomicQ().ToString("0.000"));
42            Console.WriteLine();
43
44            // Disperancy of economic factorization.
45            Console.WriteLine($"Norm(A - L * Q) = {(A - lq.EconomicL() * lq.EconomicQ()).L2Norm():E8}");
46            Console.WriteLine();
47
48            // Generate underdetermined system of linear equation and solve it.
49            Vector B = A * Vector.Random(4);
50            Vector X = lq.Solve(B);
51
52            // Print found solution.
53            Console.WriteLine("X = ");
54            Console.WriteLine(X.ToString("0.000"));
55            Console.WriteLine();
56
57            // Print error.
58            Console.WriteLine($"Error = {(B - A * X).L2Norm():E8}");
59        }
60    }
61}

See Also