Agglomerative Clustering

Agglomerative Clustering is a Hierarchical algorithm which produces tree structure of clusters proceeding iteratively to 'bottom-up' direction. The algorithm requires transforming of an object-to-variable table into an object-to-object distance matrix as a preliminary step.

Special term, Linkage Criterion, is used to denote a way to determine the distance between two sets of objects (clusters) as a function of the pairwise distances between the objects in distinct sets. The most commonly used linkage criteria are:

• Maximum over all pairwise object distances;

• Minimum over all pairwise object distances;

• Average - the mean value over all pairwise object distances.

The algorithm initially treats each of the objects as a single-element cluster and then successively merges the two closest clusters at each pass. The process (if no stopping criterion is applied) is repeated until getting a single (total) data set and results in hierarchical structure of clusters in the form of dendrogram.

Dendrograms are organized by supertype-subtype (parent-child) relationships; in such an inheritance the subtype has the same properties as the supertype plus one or more additional specific properties. Following agglomerative procedure we link more and more elements together and aggregate larger and larger clusters of increasingly dissimilar objects; in the last step all the objects are joined together.

There are two implementations of Agglomerative Algorithm in the FinMath Toolbox:

• Traditional clustering which is implemented by the AgglomerativeClustering class and has restricted performance ( O( N ³) for N objects with ready distance matrix).

  This class is not recommended to use for more than 1000 objects in real-time or simulation applications.

• Fast algorithm implemented by the SparseAgglomerativeClustering class is aimed at working with large data sets since it has increased performance estimated as O( N ²) for N objects.

  Such performance is gained due to special mechanism that accelerates data processing and requires less amount of memory. For usage convenience, it also supports the traditional mode.

Caution
Hereinafter working with raw observations should remember that the objects are assumed to be arranged in columns and presented by their features in rows.

For usability reason, the AgglomerativeClustering class always produces two sets of clusters:

• A full clusters tree (dendrogram),

• A partition which includes the desired number of clusters.

The class provides flexibility of using with different linkage criteria and metrics.

The linkage criteria are provided by the LinkageCriteria enumeration which includes the members mentioned in the section above.

The list of metrics is provided by the MetricType enumeration (see the Distance Metrics section for details).

To initialize an instance of the class there are two constructors provided to apply either the default (Minimum) or user-specific linkage criterion:

• AgglomerativeClustering(Int32)

• AgglomerativeClustering(LinkageCriteria, Int32)

The class realizes the basic interface and extends it with the method AgglomerativeTree to present dendrogram of clusters (see detailed below Presentation of Dendrogram).

The SparseAgglomerativeClustering class generally repeats the interface of the AgglomerativeClustering class with slight differences concerning to fast clustering.

The only constructor SparseAgglomerativeClustering(Int32) is provided to initialize an instance of the class.

Clustering can be performed in two modes:

• Standard, that is with the overridden ComputeClustering methods,

• Fast clustering with the specialized method ComputeClustering(Int32, SparseAgglomerativeClusteringGetMetricLineDelegate) which requires access to a distance matrix by row (or column) index via delegation mechanism. Only Single Linkage (Minimum) criterion is provided in this mode.

The basic Centroids method is not available in this implementation since the class does not operate with the whole distance matrix in fast mode.

To present clusters hierarchy, each of the classes labels all the tree nodes (objects and clusters) with numbers in natural order: first it enumerates all the objects to be clustered starting from zero and then continues the number series as new clusters appear.

The sample dendrogram below illustrates the principle of labeling, where the objects (tree leaves) are green and the generated clusters are gray; the numbers inside the nodes indicate labels and the notes above them show clusters' content (objects by numbers).

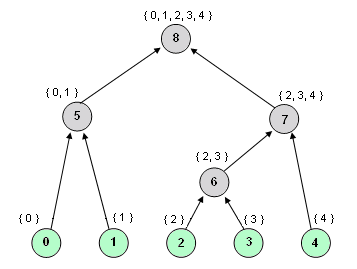
Dendrogram presentation is based on such labeling, the description and the presentation of the sample dendrogram follows:

Property

Description

AgglomerativeTree AgglomerativeTree

Returns numeric presentation of cluster hierarchy, the size of returned array equals to the total number of nodes in the dendrogram. Cluster hierarchy is coded by elements' positions and values: a given element is positioned in the array in accordance to its number (label) and the value equals to its parent number, so that the array contains numbers (labels) of parents for the nodes located in the array in accordance with their numbers. For the sample hierarchy, the property will be as follows: The nodes 0 and 1 (located by their positions 0 and 1 in the array) have the node 5 as the parent what is reflected by two numbers 5 at the positions 0 an 1, and so on. The element at the position 8 is the parent for itself since it is the root node.

The following sample demonstrates Agglomerative Clustering implementation:

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.ClusterAnalysis;
 4using FinMath.DataStructures;
 5
 6namespace FinMath.Samples
 7{
 8    class AgglomerativeClusteringSample
 9    {
10        static void Main()
11        {
12            // Input parameters
13            const int objectsCount = 7;
14            const int factorsCount = 5;
15            const int desiredClustersCount = 3;
16            const MetricType metricType = MetricType.EuclideanDistance;
17            const LinkageCriteria linkageCriteria = LinkageCriteria.Minimum;
18
19            // Generate input data matrix.
20            Matrix dataMatrix = Matrix.Random(factorsCount, objectsCount);
21
22            Console.WriteLine("Input DataMatrix: ");
23            Console.WriteLine(dataMatrix.ToString("0.000"));
24
25            // Initialize reusable clusterization performer.
26            AgglomerativeClustering clustering = new AgglomerativeClustering(linkageCriteria, desiredClustersCount);
27
28            // Perform agglomerative clustering.
29            clustering.ComputeClustering(dataMatrix, metricType);
30
31            // Get resulting numbers of clusters.
32            Int32 clusterCount = clustering.ClustersCount;
33            // Get centroids data matrix. Each line describe centroid of one cluster.
34            Matrix centroids = clustering.Centroids();
35            // Get central elements list.
36            IntegerArray centralElements = clustering.CentralElements();
37
38            if (clustering.Status == FMStatus.MethodSucceeded)
39            {
40                Console.WriteLine();
41                Console.WriteLine("Clustering computed successfully. Test Result:");
42                Console.WriteLine("  Number of clusters: " + clusterCount);
43                // Output clusters assignment. i-th element contains number of cluster assigned to i-th object
44                Console.WriteLine("  Cluster assignment: " + clustering.ClustersAssignment());
45                // Output clusters hierarchy. i-th element contains parent node for i-th node.
46                // First 8 nodes corresponds to input elements. Others generated as product as linkage.
47                Console.WriteLine("  Cluster agglomerative tree: " + clustering.AgglomerativeTree());
48                Console.WriteLine();
49
50                for (Int32 i = 0; i < clusterCount; ++i)
51                {
52                    Console.WriteLine("Cluster #" + (i + 1));
53                    // Output elements of i-th cluster.
54                    Console.WriteLine("  Cluster elements: " + clustering.GetCluster(i + 1));
55                    // Output central element of i-th cluster.
56                    Console.WriteLine("  Cluster central element: " + centralElements[i]);
57                    // Output centroid of i-th cluster.
58                    Console.WriteLine("  Cluster centroid " + centroids.GetRow(i).ToString("0.000"));
59                }
60            }
61            else
62                Console.WriteLine("Clustering computation failed.");
63        }
64    }
65}

Reference

Other Resources