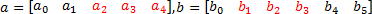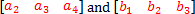Click or drag to resize

Distance Metrics

Clustering algorithms utilize metrics of different nature depending upon application domain and classification scheme.

Distance Metrics provided

The FinMath Toolbox provides several metrics applied to any two objects, A and B, presented as points in multi-dimensional space of objects' features. The metrics provided are listed in the MetricType enumeration.

Metrics are implemented as methods of the MetricsCalculator class which can produce metrics as for single pairs of multi-dimensional point as well for series of such points.

Caution note Caution

Format of input data is the same for all the methods and assumes rows corresponding to variables (features) and columns corresponding to to objects (observations). So the distances are computed between the columns.

The class includes only static methods that are ether metric-specific or common (i.e. suitable to produce any of the predefined metrics). With that, it realizes the Extension Methods mechanism which makes available any metric-specific method as an instance method. The following types of methods are provided calculating distance between:

  • two Vector objects,

    the result is of type Double;

  • objects represented as Matrix columns;

    the result is a Matrix, [i,j] element is the distance between i-th and j-th columns;

  • two object sets, each one represented as a Matrix (matrix is a set of columns);

    the result is a Matrix, [i,j] element is the distance between i-th column of the first matrix and j-th column of the second one;

  • two one-dimensional arrays of Double[] values;

    the result is of type Double;

  • two parts of one-dimensional arrays of Double[] values, each part specified by an offset in the array, and by the size of the offsets:

    Suppose the arrays are: Cluster Arrays

    with offsets 2 and 1 respectively, and with size 3, then the distance will be calculated between:

    Cluster Offsets

    the result is of type Double;

To make instance methods available, the FinMath.ClusterAnalysis namespace should be declared with using directive: using FinMath.ClusterAnalysis;

Metric-specific methods are:

Metric

Description

Squared Euclidean distance

The sum of squared differences along all coordinates: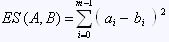

Cluster Squared Euclidian

StaticSquaredEuclideanDistance(Matrix)

StaticSquaredEuclideanDistance(Matrix, Matrix)

StaticSquaredEuclideanDistance(Vector, Vector)

StaticSquaredEuclideanDistance(Double, Double)

StaticSquaredEuclideanDistance(Double, Int32, Double, Int32, Int32)

Euclidean distance

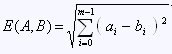
Cluster Euclidian

StaticEuclideanDistance(Matrix)

StaticEuclideanDistance(Matrix, Matrix)

StaticEuclideanDistance(Vector, Vector)

StaticEuclideanDistance(Double, Double)

StaticEuclideanDistance(Double, Int32, Double, Int32, Int32)

Cityblock distance

Manhattan distance

The sum of the absolute differences along all coordinates: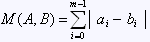

Cluster Manhattan

StaticManhattanDistance(Matrix)

StaticManhattanDistance(Matrix, Matrix)

StaticManhattanDistance(Vector, Vector)

StaticManhattanDistance(Double, Double)

StaticManhattanDistance(Double, Int32, Double, Int32, Int32)

Hamming distance

Being adapted to vectors of real numbers, this metric is defined as the averaged number of positions at which the corresponding vectors are different: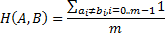

Cluster Hamming

StaticHammingMetric(Matrix)

StaticHammingMetric(Matrix, Matrix)

StaticHammingMetric(Vector, Vector)

StaticHammingMetric(Double, Double)

StaticHammingMetric(Double, Int32, Double, Int32, Int32)

Chebyshev distance

Infinity distance

Defines the distance between two vectors as the greatest of their absolute differences along any coordinate: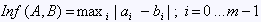

Cluster Infinity

StaticInfinityDistance(Matrix)

StaticInfinityDistance(Matrix, Matrix)

StaticInfinityDistance(Vector, Vector)

StaticInfinityDistance(Double, Double)

StaticInfinityDistance(Double, Int32, Double, Int32, Int32)

Correlation distance

Mantegna distance

Mantegna metric converts correlation into distance: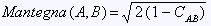

Cluster Mantegna
where C AB is the correlation coefficient between the vectors (or matrix rows) A and B.
Note Note

It is easy to see that in the case of complete positive correlation ( C AB = 1 ) the distance is zero, for uncorrelated time series ( C AB = 0 ) it equals to Cluster Root Of Two and in the case of complete negative correlation ( C AB = -1 ) the distance is two.

Methods to compute metric from observations:

StaticMantegnaMetric(Matrix)

StaticMantegnaMetric(Matrix, Matrix)

StaticMantegnaMetric(Vector, Vector)

StaticMantegnaMetric(Double, Double)

StaticMantegnaMetric(Double, Int32, Double, Int32, Int32)

Methods to compute metric from correlations, either with replacing of the input correlation matrix (that is, it becomes the distance matrix) or not:

StaticMantegnaMetricFromCorrelation(Matrix)

StaticMantegnaMetricFromCorrelation(Double)

StaticMantegnaMetricFromCorrelationInPlace(Matrix)

StaticMantegnaMetricFromCrossCorrelation(Matrix)

StaticMantegnaMetricFromCrossCorrelationInPlace(Matrix)

Cosine distance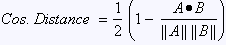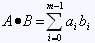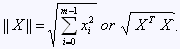

Cluster Cosin Distance
where:
Cluster AdotB
Cluster NormX
Note Note

This metric results in the range [0, 1] so that 0 means exactly the same and 1 means the maximal distance.

StaticCosineSimilarity(Matrix)

StaticCosineSimilarity(Matrix, Matrix)

StaticCosineSimilarity(Vector, Vector)

StaticCosineSimilarity(Double, Double)

StaticCosineSimilarity(Double, Int32, Double, Int32, Int32)

 

The common methods are:

take an additional input parameter, one of items listed in the MetricType, which specifies one of the metrics described above.

 

Note Note

Computing of distances is resource consuming operation estimated as O(MN2) where N is the number of the objects and M is the number of the variables.

Code Sample

Distance calculation example:

C#
Copy
 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.ClusterAnalysis;
 4
 5namespace FinMath.Samples
 6{
 7    class DistanceMetrics
 8    {
 9        static void Main()
10        {
11            // Input parameters
12            const int factorsCount = 5;
13
14            // Create two input vectors.
15            Matrix xyMatrix = Matrix.Random(factorsCount, 2);
16            // Prepare variants of input data.
17            Vector xVector = xyMatrix.GetColumn(0);
18            Vector yVector = xyMatrix.GetColumn(1);
19            Matrix xMatrix = xVector.ToColumnMatrix();
20            Matrix yMatrix = yVector.ToColumnMatrix();
21            Double[] xArray = xVector.ToArray();
22            Double[] yArray = yVector.ToArray();
23
24            Console.WriteLine("Input vectors:");
25            Console.WriteLine("  First vector:  " + xVector.ToString("0.000"));
26            Console.WriteLine("  Second vector: " + yVector.ToString("0.000"));
27
28            Console.WriteLine();
29            Console.WriteLine("Results:");
30            Console.WriteLine("    Distances metric name | Vector | Array | Offset Array | Matrix | Matrices |");
31            // Enumerate all types metric. Note, due to existing aliases for some metric we will get repetitions.
32            foreach (MetricType metric in Enum.GetValues(typeof(MetricType)))
33            {
34                // Calculate distance between two vectors.
35                Double vectorMetric = xVector.CalculateMetric(yVector, metric);
36                // Calculate distance between two arrays.
37                Double arrayMetric = xArray.CalculateMetric(yArray, metric);
38                // Calculate distance between two arrays starting from offsets and use specified number of factors.
39                Double offsetArrayMetric = MetricsCalculator.CalculateMetric(xArray, 0, yArray, 0, 5, metric);
40                // Calculate distance between columns of matrix. We get element [0, 1] which means distance between column #0 and column #1.
41                Double matrixMetric = xyMatrix.CalculateMetric(metric)[0, 1];
42                // Calculate distance between columns of two matrices. 
43                // We get element [0, 0] which means distance between column #0 from first matrix and column #0 from second matrix.
44                Double matricesMetric = xMatrix.CalculateMetric(yMatrix, metric)[0, 0];
45
46                // Output results.
47                Console.WriteLine($"{metric,25} | {vectorMetric,6:0.000} | {arrayMetric,5:0.000} | {offsetArrayMetric,12:0.000} | {matrixMetric,6:0.000} | {matricesMetric,8:0.000} |");
48            }
49        }
50    }
51}

See Also