Base Terms and Concepts

The key term in the domain is Cluster. Depending on the area of application, Clusters can be denoted with synonymic or close-meaning terms: partitions, taxa (plural form of taxon), classes or categories.

Clusters are mathematically defined as such non-empty subsets of a data set X that the following conditions are met:

• These subsets are non-overlapping (each of the elements of the data set X belongs to only one cluster) and, hence, mutually exclusive as the intersection of any two clusters is empty;Item 1

• The union of the clusters is equal to the data set X (the clusters are said to cover X or collectively exhaustive).

In an even wider classification context, clusters are sort of so called library classification system which organizes homogeneous objects into groups in a hierarchical tree structure, so that every object is assigned to only one group and belongs also only to its super-groups in hierarchy; multi-parents relationships besides the nested hierarchy are not allowed.

Note
A different kind of classification system, called a faceted classification system, allows the assignment of multiple classifications to an object, enabling the classifications to be ordered in multiple ways and so can not be done with clustering algorithm.

Usual form of a data set X presentation is a matrix where one dimension corresponds to objects (observations) and the other corresponds to variables. Most often, subject of clustering are objects (such terms as case, item, entity or instance are in use as synonymous to 'object') presented as data points in space of variables (the variables are called also features, attributes, characteristics or parameters). Clustering of variables (time series) is also in use.

Evidently, the variables should encode as much information as possible to distinct the objects in context of the area of interest. Ideally, properly selected features should result in clusters revealing not only formal but real hidden relationships between the objects.

Classification is originally an identification problem and means assignment of newly observed objects to the a-priory known set of clusters, so that the objects assigned to the same cluster are similar in some sense. Clusters are usually presented by their aggregative patterns based on information extracted beforehand from the previously observed and classified objects.

Clustering is aimed at revealing clusters (classifications) in observed real-world data given no training patterns; it is a learning procedure that detects specific characteristics of the clusters underlying the data set and establishes itself the clusters based on their intrinsic regularities. Since the resulting clusters are presented by the classified objects, clustering is considered as data-driven automatic classification (or unsupervised pattern recognition) and this is why the term classification is in use in some areas as synonymous with what is commonly known as clustering.

Clustering algorithm generally consists of:

• An extraction mechanism that computes explicit criterial parameters from the observations to use for comparative evaluation of the objects; major criterial parameters for clustering are 'similarities' between any two objects presented in a suitable metric. Cluster metric serves as a sensor in clustering algorithm;

• A classification scheme (learning technique) that does the actual job of classifying objects, relying on the extracted metrics. A particular scheme is usually based on an operational decision rule for identification of the objects as belonging to the corresponding clusters; this rule implements a particular classification criterion and is said to be classifier.

Standard steps in clustering are:

1. Selection of informative features for the objects to be clustered;

2. Defining a proximity measure;

3. Defining clustering criterion and scheme;

4. Validation, interpretation and application of the results.

With the FinMath Toolbox, user is only focused on external aspects of the problem, namely, features selection (step 1) and applying of the results (step 4), being provided with the algorithms presented further.

The most general systematization of clustering algorithms is based on the type of cluster structure to be discovered. According to output type, there are Partitioning algorithms and Hierarchical algorithms.

Partitioning algorithms (sometimes called hard or crisp clustering) typically produce all clusters at once as a set of non-empty and non-intersecting subsets that cover the data set.

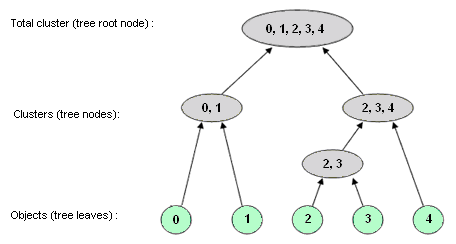
Unlike partitioning, Hierarchical algorithms result in a hierarchical tree structure of classifications for a given set of objects like the figured below:

Reference

Other Resources