K-Means Clustering

K-Means is Partitioning algorithm which takes as input a positive integer number of clusters K and a data set to divide into K non-empty, non-overlapping and non-subordinated clusters.

In its essence, K-Means is an optimization iterative algorithm whose general logic is stepwise positioning of K clusters' centroids in densely populated regions of the data space, until some stop criterion triggers. The centroids serve as centers of gravity to merge objects into clusters such that objects within each cluster are as close to each other as possible, and as far from objects in other clusters as possible.

The target function to minimize while clustering is the sum of object-to-centroid distances, summed over all K clusters:

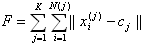
• N( j ) is the number of objects in the j-th cluster;

• x_i^{( j )} is the i-th object belonging to the j-th cluster, i = 1 .. N( j );

• c _j is the centroid of the j-th cluster;

• ||...|| denotes the distance using the metric selected.

The algorithm proceeds in two phases:

1. Initialization. Given the number K of clusters, initialization means creating an initial partition by assigning somehow all the objects to K clusters, and computing the initial cluster centroids.

   Usual initial partition divides the objects into K clusters randomly. Appropriate initializing can play a big effect in K-Means (see Restrictions and Recommendations for details).

2. Partitioning itself is two-step iterative procedure for each object:

   • Assignment step, where the distances of the object from the centroids of each of K clusters are computed; if the object in not currently in the cluster with the closest prototype, then it is reassigned to its nearest cluster.

   • Update step: if reassignment occurs, both the clusters (the gaining the new object and the loosing the object) are updated and their centroids are recalculated using the current memberships; if this decreases the target function then the reassignment is established, what means moving of the clusters in more densely populated regions of the data space.

   The Assignment and Update refinement steps are repeated until convergence is achieved; typical convergence criteria are: no (or minimal) reassignment of objects to new clusters, minimal decrease in target function or simply maximal number of iterations.

Although the K-Means algorithm is widely used due to its computational performance, it suffers from the two significant drawbacks when applied to real world applications:

1. The user has to define the value of K, the number of clusters, although this is really one of the objectives of clustering, and it is not easy for high-dimension data if there are no clues as to what number of clusters might be appropriate. Choosing an inappropriate number of clusters will lead to a meaningless typology.

   The simplest recommendation (rule of thumb) sets the number to , where N is is the number of objects. Known heuristic recommendations usually include complex experimental approaches like trying several values of K or preliminary hierarchical clustering.

   For more systematic approach refer to this source as a start point.

2. The K-Means algorithm reaches a local minimum, but cannot guarantee the global minimum of the criterion what results in high sensitivity to initial conditions. For a given K, clusters depend significantly on the initial configuration of the set of centroids, thus making interpretation of the clusters rather uncertain. As a particular case there is also problem of 'dead' centroids: when some centroid is initialized far away from the input data set in comparison to other centroids, it becomes not utilized for any calculation and never appropriate for any cluster.

   Common recommendations at this point are:

   • Using K-Means if there is enough volume of data available;

   • Using expert knowledge at initialization step;

   • Using several replicates with random starting points.

Caution
Hereinafter working with raw observations should remember that the objects are assumed to be arranged in columns and presented by their features in rows.

The K-Means algorithm is implemented by the KMeans class. The implementation utilizes the maximal number of iterations as stop criterion and either random (default) or custom initialization of clusters; custom initialization is provided for using expert knowledge to overcome high sensitivity to initial conditions.

The only constructor, KMeans(Int32, Int32), requires two input parameters: the number of clusters K and the maximal number of iterations to stop clustering procedure.

Note
The input number of clusters, K, is interpreted as 'no more than', i.e. the resulting number of clusters can be less than K.

Given the class instance initialized, user can define an initial distribution of the objects between K clusters before running of clustering procedure; if no cluster initialization is done then the objects will be distributed randomly. Clusters initialization is available via the SetClustersAssignment(IntegerArray) method according to assignment rules (see Basic Methods)

The class provides all the Basic Methods and Properties and one more, the Iterations property, which shows the number of iterations actually performed while clustering.

K-Means Clustering usage:

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.ClusterAnalysis;
 4using FinMath.DataStructures;
 5
 6namespace FinMath.Samples
 7{
 8    class KMeansSample
 9    {
10        static void Main()
11        {
12            // Input parameters
13            const int objectsCount = 7;
14            const int factorsCount = 5;
15            const int desiredClustersCount = 3;
16            const int stepLimit = 100;
17            const MetricType metricType = MetricType.EuclideanDistance;
18
19            // Generate input data matrix contains.
20            Matrix dataMatrix = Matrix.Random(factorsCount, objectsCount);
21            // Generate default clustering assignment.
22            // Randomly assign each of object to one of clusters.
23            // You do not need to do it yourself it will be done by default. 
24            // It just shows how can you set start assignment if you know some reasonable one.
25            IntegerArray defaultAssignment = IntegerArray.Random(objectsCount, 1, desiredClustersCount + 1);
26
27            Console.WriteLine("Input DataMatrix: ");
28            Console.WriteLine(dataMatrix.ToString("0.000"));
29            Console.WriteLine("Default assignment: " + defaultAssignment);
30
31            // Initialize reusable clusterization performer.
32            KMeans clustering = new KMeans(desiredClustersCount, stepLimit);
33
34            // Here we set default cluster assignment.
35            clustering.SetClustersAssignment(defaultAssignment);
36
37            // Perform KMeans clustering.
38            // We use Euclidean distance to construct distance matrix.
39            clustering.ComputeClustering(dataMatrix, metricType);
40
41            // Get resulting numbers of clusters.
42            Int32 clusterCount = clustering.ClustersCount;
43            // Get centroids data matrix. Each line describe centroid of one cluster.
44            Matrix centroids = clustering.Centroids();
45            // Get central elements list.
46            IntegerArray centralElements = clustering.CentralElements();
47
48            if (clustering.Status == FMStatus.MethodSucceeded)
49            {
50                Console.WriteLine();
51                Console.WriteLine("Clustering computed successfully. Test Result:");
52                Console.WriteLine("  Number of clusters: " + clusterCount);
53                // Output clusters assignment. i-th element contains number of cluster assigned to i-th object
54                Console.WriteLine("  Cluster assignment: " + clustering.ClustersAssignment());
55                Console.WriteLine();
56
57                for (Int32 i = 0; i < clusterCount; ++i)
58                {
59                    Console.WriteLine("Cluster #" + (i + 1));
60                    // Output elements of i-th cluster.
61                    Console.WriteLine("  Cluster elements: " + clustering.GetCluster(i + 1));
62                    // Output central element of i-th cluster.
63                    Console.WriteLine("  Cluster central element: " + centralElements[i]);
64                    // Output centroid of i-th cluster.
65                    Console.WriteLine("  Cluster centroid " + centroids.GetRow(i).ToString("0.000"));
66                }
67            }
68            else
69                Console.WriteLine("Clustering computation failed.");
70        }
71    }
72}

Reference

Other Resources