Click or drag to resize

Basics Of Implementations

This topic contains the following sections:

For usability reason, the variety of the clustering algorithms implemented in the FinMath Toolbox has the same basic features and provides uniform way of using and interpretation of clustering results.

Every particular class overrides the base properties and methods if they are applicable in accordance to the specific algorithm.

Representation of Objects and Clusters

In all the implementations objects and clusters are represented by their numbers (indices): at the beginning of clustering procedure the objects are enumerated starting from zero, and the clusters are enumerated starting from one in the order they appear.

The figure below is the sample partition to demonstrate how the objects and the clusters are coded.

Cluster Sample Impl

In the example, there are eight (green) objects from 0 to 7 distributed among the four (gray) clusters from 1 to 4.

Note Note

Hierarchies of clusters are coded similarly to partitions in that implementations where they can be produced (see Agglomerative Clustering).

Basic Methods

Basic methods provide general ways to perform clustering and access the results in suitable forms.

Caution note Caution

Hereinafter working with raw observations should remember that the objects are assumed to be arranged in columns and presented by their features in rows.

Method

Description

methodComputeClustering(Matrix)

methodComputeClustering(Matrix, MetricType)

Methods to run clustering procedure either with a distance matrix or with a raw observations matrix and user-specific metric.

The methods indicate successful clustering with the returned true value and also modify the Status property. These methods are standardly used in all the implementations.

methodClustersAssignment

Returns the description of how the objects are grouped into the clusters.

For the sample, the returned array will be:

Cluster Sample Assign
The objects 0 and 1 (identified respectively by the positions 0 and 1) go into the first cluster (1 at the positions 0 and 1 in the array), the next three objects go into the second cluster, and so on.

methodGetCluster(Int32)

Returns the addressed cluster as an array of members presented by their indices.

For the sample, consecutive calls of the method with indices from one to ClustersCount will present the following explicit description of the clusters:

Index

Cluster

1

{0, 1}

2

{2, 3, 4}

3

{5}

4

{6, 7}

methodCentroids

Computes a matrix of virtual cluster representatives in original features space; [i,j] element of the matrix represents j-th factor of the centroid of the i-th cluster. In our example it is: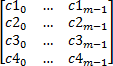

Cluster Centroids

where c1, c2, c3, and c4 are the centroids of corresponding clusters.

Depending on the metric utilized, the method applies a suitable averaging technique to compute aggregative values of each variable over the objects in the cluster.

Note Note

  • This method is available only if clustering procedure was performed over an variable-to-object data matrix (not distance matrix).

  • The method is not applicable with the SparseAgglomerativeClustering class.

methodCentralElements

In each cluster, the method calculates pairwise distances between all the members and detects that central member which has minimal summary distance to other cluster members.

Index of the central member is inserted into the returned array at the corresponding cluster's position.

Basic Properties

The are two basic properties for all the implementations:

Property

Description

PropertyStatus

Computation status: takes the MethodSucceeded value if clustering converges.

PropertyClustersCount

Returns the actual number of clusters in the resulting partition.

For the sample this value equals to 4.

See Also