Matrix Norms |
Hereinafter the following convention is used:
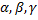– small Greek letters are used to denote scalars;
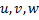– small Latin letters are used to denote vectors;
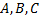– capital Latin letters are used to denote matrices.
MethodsThis section describes methods applied to compute matrix norm.
Operation | Description | Performance |
|---|---|---|
L1 norm (Taxicab norm, Manhattan norm) | Computes the L1 norm of the matrix. 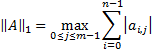 which is simply the maximum absolute column sum of the matrix. | |
L2 norm (Euclidean norm) | Computes the L2 norm of the matrix. 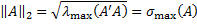 It is the largest singular value of A or the square root of the largest eigenvalue of A'A. A' denotes the transpose of A. | |
infinity norm | Computes the infinity norm of the matrix. 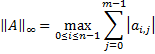 which is simply the maximum absolute row sum of the matrix. | |
Frobenius norm | Computes the Frobenius norm of the matrix. 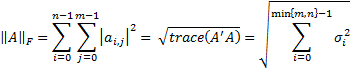 which is simply the maximum absolute row sum of the matrix. | |
max norm | Computes the max norm (maximal absolute value of matrix' elements).  |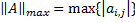
Besides there is a common method Norm that allows to specify the desirable matrix norm as a parameter. It computes one of the above described norms of the matrix.
See Also