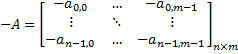Algebraic Operations |
Hereinafter the following convention is used:
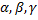 – small Greek letters are used to denote scalars;
– small Greek letters are used to denote scalars;
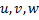 – small Latin letters are used to denote vectors;
– small Latin letters are used to denote vectors;
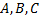 – capital Latin letters are used to denote matrices.
– capital Latin letters are used to denote matrices.
This topic contains the following sections:
This section describes methods implementing unary operations, i.e. operations performed with one matrix.
Operation | Description | Performance |
|---|---|---|
plus | Creates a copy of the original matrix. Actually, PlusInPlace() method does nothing. In place:Returning result:Out of place: | |
minus |
Negates this matrix. If the matrix is
then the result of this operation will be |
Addition operation allows adding a matrix or a scalar to the given matrix.
Operation | Description | Performance |
|---|---|---|
matrix-scalar addition | Calculates the sum of a scalar and a matrix (or a matrix and a scalar – as you know the addition is commutative operation). This operation is defined as: given: 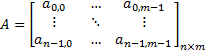 then: 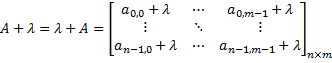 | |
matrix-matrix addition | Adds the given matrix to this matrix. This operation is defined as: given: 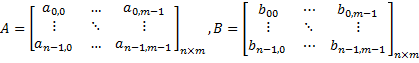 then: 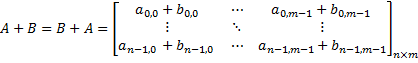 |
Subtraction allows calculating the difference between a matrix and a scalar or between two matrices.
Operation | Description | Performance |
|---|---|---|
matrix-scalar subtraction | The difference of a matrix and a scalar: 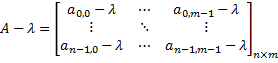 The difference of a scalar and a matrix: 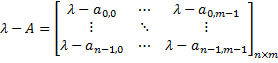 | |
matrix-matrix subtraction | The difference of the given matrix and another matrix: 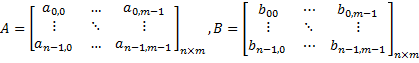 then: 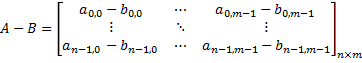 The opposite operation: 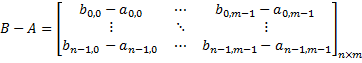 |
Multiplication of a matrix by a scalar, a vector or a matrix.
Operation | Description | Performance |
|---|---|---|
matrix-scalar multiplication | Multiplies this matrix by the given scalar: 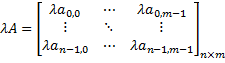 | |
matrix-vector multiplication | Multiplies this matrix by the column vector from the right. Consider the given vector is: 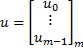 The result will be: 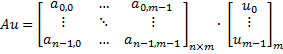 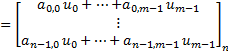 Multiplies this matrix by the row vector from the left. Consider the given vector is: 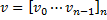 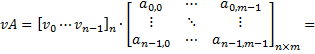 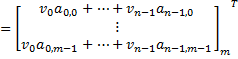 | |
matrix-matrix multiplication | Multiplies this matrix by the given matrix from the right. Consider the given matrix is: 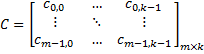 The result will be: 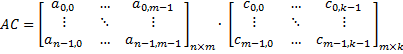 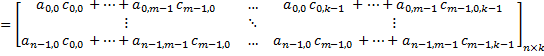 Multiplies this matrix by the given matrix from the left. Consider the given matrix is: 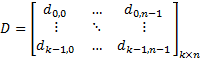 The result will be: 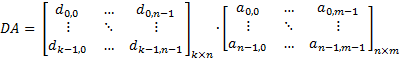 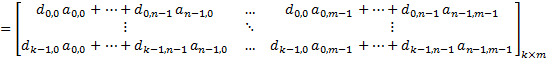 |
Division of a matrix by a scalar.
Operation | Description | Performance |
|---|---|---|
matrix-scalar division | Divides each element of the matrix by the given scalar: 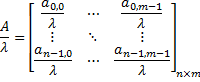 |
The described algebraic operations methods can be replaced by mathematical signs of this operations: +, -, *, / like in example below:
1Matrix A = new Matrix(4); 2Matrix B = new Matrix(4); 3 4// Sum of matrices. 5Matrix C = A + B; 6 7// Sum of a matrix and a scalar. 8Matrix D = A + 2.0;