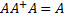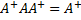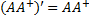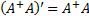Transposition, Normalization, Inversion |
Hereinafter the following convention is used:
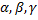– small Greek letters are used to denote scalars;
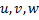– small Latin letters are used to denote vectors;
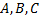– capital Latin letters are used to denote matrices.
This topic contains the following sections:
TranspositionThe transpose of a matrix A is another matrix A':
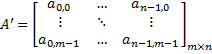
Formally, the (i,j) element of A' is the (j,i) element of A:
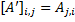
Operation | Description | Performance |
|---|---|---|
transpose | Computes the transpose of this matrix. In place:Out of place:Returning result: |
NormalizationA matrix is normalized if its norm is equal to 1. User must specify the norm type as a parameter of normalization method.
Operation | Description | Performance |
|---|---|---|
normalize | Normalizes this matrix (with unity norm). In place:Out of place:
|
InversionSquare n-by-n matrix A is invertible if there exists an n-by-n matrix B such that their product is n-by-n identity matrix:
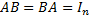
Operation | Description | Performance |
|---|---|---|
invert | Inverts this matrix (using LU decomposition). In place:Out of place:Returning result: |
Pseudoinversion
The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse. A Moore–Penrose pseudoinverse (hereafter, just pseudoinverse) of A is defined as a matrix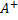 
,
satisfying all of the following four criteria:
Operation | Description | Performance |
|---|---|---|
pseudoinverse | Computes the Moore-Penrose pseudoinverse matrix. In place:Out of place:Returning result:This routine uses advanced algorithm that performs much faster for most matrices: In place:Out of place:Returning result: |
See Also