ChiSquare

The chi-square distribution (also chi-squared or χ²-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. It is one of the most widely used probability distributions in inferential statistics, e.g., in hypothesis testing or in construction of confidence intervals.

ChiSquare class inherits from the Gamma class.

This topic contains the following sections:

Constructor
Methods
Properties

Constructor

Constructor	Description	Performance
set number of degrees of freedom	Creates new instance of chi-square with user specified parameters. ChiSquare(Double)

Description

Performance

set number of degrees of freedom

Creates new instance of chi-square with user specified parameters.

method ChiSquare(Double)

Methods

Method	Description	Performance
sample	Static method which generates new sample of Chi-square distribution variate with specified parameters. Sample(Double)
pdf	Probability density function. 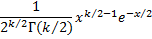where Γ(k/2) denotes the Gamma function. Static probability density function. Pdf(Double, Double)
cdf	Cumulative distribution function. 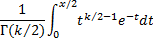Static cumulative distribution function. Cdf(Double, Double)
inverse cdf	Inverse cumulative distribution function. Is useful for quantile calculation. Function will return value of random variable such that likelihood for this random variable to occur less than or equal to returned value equal to specified pvalue parameter. InverseCdf(Double, Double)

Properties

Property	Description	Performance
number of degrees of freedom	DegreesOfFreedom

See also inherited methods and properties in the description of parent Gemma class.