Uniform |
The continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable.
The support is defined by the two parameters, a and b, which are its minimum and maximum values. The distribution is often abbreviated U(a,b). It is the maximum entropy probability distribution for a random variate X under no constraint other than that it is contained in the distribution's support.
This topic contains the following sections:
Constructor | Description | Performance |
|---|---|---|
set bounds | Creates new instance of continuous uniform distribution with user specified parameters. |
Method | Description | Performance |
|---|---|---|
sample | Generate random variable sample. Fill in array with random variable series in place: Static method which generates new sample of Uniform distribution variate with specified parameters: | |
Probability density function. 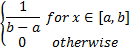 Static probability density function. | ||
cdf | Cumulative distribution function. 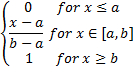 Static cumulative distribution function. | |
inverse cdf | Inverse cumulative distribution function. Is useful for quantile calculation. Function will return value of random variable such that likelihood for this random variable to occur less than or equal to returned value equal to specified pvalue parameter. |
Property | Description | Performance |
|---|---|---|
left bound | Left bound of distribution interval. | |
right bound | Right bound of distribution interval. | |
mean | Mean of the distribution. 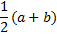 | |
median | Median of the distribution. 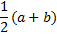 | |
mode | Mode of distribution. 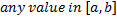 | |
kurtosis | Excess Kurtosis of distribution. 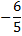 | |
skewness | Skewness of distribution. 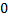 | |
entropy | Entropy of distribution. 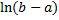 | |
variance | Variance of the distribution. 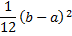 |


