Laplace |
the Laplace distribution is a continuous probability distribution. The difference between two independent identically distributed exponential random variables is governed by a Laplace distribution, as is a Brownian motion evaluated at an exponentially distributed random time. This distribution has two parameters: scale b and mean μ.
This topic contains the following sections:
ConstructorConstructor | Description | Performance |
|---|---|---|
set scale and mean | Creates new instance of Laplace with user specified parameters. | |
set random generator | Creates new instance of Laplace with user specified generator and parameters. |
MethodsMethod | Description | Performance |
|---|---|---|
sample | Generate random variable sample. Fill in array with random variable series in place: Static method which generates new sample of Laplace distribution variate with specified parameters: | |
Probability density function. 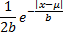 Static probability density function. | ||
cdf | Cumulative distribution function. 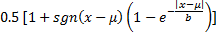 Static cumulative distribution function. | |
inverse cdf | Inverse cumulative distribution function. Is useful for quantile calculation. Function will return value of random variable such that likelihood for this random variable to occur less than or equal to returned value equal to specified pvalue parameter. |
PropertiesProperty | Description | Performance |
|---|---|---|
scale | Scale of the distribution. | |
mean | Mean of the distribution.  | |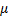
median | Median of the distribution. | |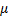
mode | Mode of distribution. | |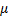
kurtosis | Excess Kurtosis of distribution.  | |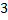
skewness | Skewness of distribution.  | |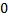
entropy | Entropy of distribution.  | |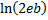
variance | Variance of the distribution.  | |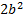
standard deviation | Standard deviation of the distribution.  |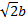
