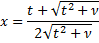TDistribution

Student’s t-distribution (or simply the t-distribution) is a continuous probability distribution that arises when estimating the mean of a normally distributed population in situations where the sample size is small and population standard deviation is unknown.

The t-distribution is symmetric and bell-shaped, like the normal distribution, but has heavier tails, meaning that it is more prone to producing values that fall far from its mean. The parameter of this distribution is the number of degrees of freedom ν.

This topic contains the following sections:

Constructor
Methods
Properties

Constructor

Constructor	Description	Performance
set degrees of freedom	Creates new instance of TDistribution. TDistribution(Double)

Description

Performance

set degrees of freedom

Creates new instance of TDistribution.

method TDistribution(Double)

Methods

Method	Description	Performance
pdf	Probability density function. 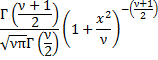where Γ denotes the Gamma function. Pdf(Double) Static probability density function. Pdf(Double, Double)
cdf	Cumulative distribution function. where I_x is the regularized incomplete beta function, , and t is the parameter of cdf. Cdf(Double) Static cumulative distribution function. Cdf(Double, Double)
inverse cdf	Inverse cumulative distribution function. Is useful for quantile calculation. Function will return value of random variable such that likelihood for this random variable to occur less than or equal to returned value equal to specified pvalue parameter. InverseCdf(Double) InverseCdf(Double, Double)

Method

Description

Performance

pdf

Probability density function.

where Γ denotes the Gamma function.

method Pdf(Double)

Static probability density function.

Static Pdf(Double, Double)

cdf

Cumulative distribution function.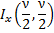

where I_x is the regularized incomplete beta function, DTDistributionX , and t is the parameter of cdf.

method Cdf(Double)

Static cumulative distribution function.

Static Cdf(Double, Double)

inverse cdf

Inverse cumulative distribution function. Is useful for quantile calculation. Function will return value of random variable such that likelihood for this random variable to occur less than or equal to returned value equal to specified pvalue parameter.

method InverseCdf(Double)

Static InverseCdf(Double, Double)

Properties

Property	Description	Performance
degrees of freedom	Degrees of freedom of the distribution. DegreesOfFreedom
mean	Mean of the distribution. Mean
median	Median of the distribution. 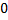Median
mode	Mode of distribution. 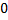Mode
kurtosis	Excess Kurtosis of distribution. 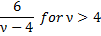Kurtosis
skewness	Skewness of distribution. 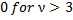Skewness
variance	Variance of the distribution. 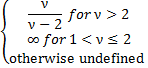Variance
standard deviation	Standard deviation of the distribution. StandardDeviation