Multinomial Logistic Regression

In statistics, logistic regression or logit regression is a type of probabilistic statistical classification model. It is used to predict the probabilities of the different possible outcomes of a categorically distributed dependent variable based on one or more predictor variables (features) which may be real-valued, binary-valued, categorical-valued, etc.

The probabilities describing the possible outcomes of a single trial are modeled, as a function of the explanatory (predictor) variables, using a logistic function. Frequently "logistic regression" is used to refer specifically to the problem in which the dependent variable is binary—that is, the number of available categories is two—and problems with more than two categories are referred to as multinomial logistic regression.

Multinomial logistic regression is known by a variety of other names, including multiclass LR, multinomial regression, softmax regression, multinomial logit, maximum entropy (MaxEnt) classifier, conditional maximum entropy model.

Multinomial logistic regression is used when the dependent variable in question is nominal (equivalently categorical, meaning that it falls into any one of a set of categories which cannot be ordered in any meaningful way) and for which there are more than two categories. Some examples would be:

• Which blood type does a person have, given the results of various diagnostic tests?

• In a hands-free mobile phone dialing application, which person's name was spoken, given various properties of the speech signal?

• Which candidate will a person vote for, given particular demographic characteristics?

Assumptions:

• The multinomial logit model assumes that data are case specific; that is, each independent variable has a single value for each case.

• The multinomial logit model also assumes that the dependent variable cannot be perfectly predicted from the independent variables for any case.

• As with other types of regression, there is no need for the independent variables to be statistically independent from each other (unlike, for example, in a naive Bayes classifier); however, collinearity is assumed to be relatively low, as it becomes difficult to differentiate between the impact of several variables if they are highly correlated.

• If the multinomial logit is used to model choices, it relies on the assumption of independence of irrelevant alternatives (IIA), which is not always desirable. This assumption states that the odds of preferring one class over another do not depend on the presence or absence of other "irrelevant" alternatives.

• If the multinomial logit is used to model choices, it may in some situations impose too much constraint on the relative preferences between the different alternatives. This point is especially important to take into account if the analysis aims to predict how choices would change if one alternative was to disappear (for instance if one political candidate withdraws from a three candidate race).

As in other forms of linear regression, multinomial logistic regression uses a linear predictor function f(k,i) to predict the probability that observation i has outcome k, of the following form:

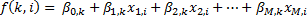
where β_m,k is a regression coefficient associated with the m-th explanatory variable and the k-th outcome. As explained in the logistic regression article, the regression coefficients and explanatory variables are normally grouped into vectors of size M+1, so that the predictor function can be written more compactly:

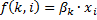
where β_k is the set of regression coefficients associated with outcome k, and x_i (a row vector) is the set of explanatory variables associated with observation i.

The unknown parameters in each vector β_k are found using iteratively reweighted least squares (IRLS).

Regressors is an N-by-P design matrix with N observations on P predictor variables:

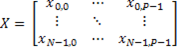
Regressands is an N-by-K matrix, where Regressands(i,j) is the number of outcomes of the multinomial category j for the predictor combinations given by Regressors.Rows(i):

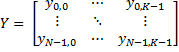
The result β is a (P+1)-by-(K-1) matrix of estimates, where each column corresponds to the estimated intercept term and predictor coefficients, one for each of the first (K-1) multinomial categories. The estimates for the K-th category are taken to be zero:

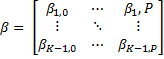
Multinomial logistic regression is implemented by the MultinomialRegression class.

To initialize a class instance use the constructor:

MultinomialRegression(Matrix, Matrix) - creates a class instance and builds regression for the input observations.

The class provides the following methods:

Operation	Description	Performance
Compute probabilities	Computes predicted probabilities for the multinomial logistic regression model with predictor X, vector with P predictor variables. Second parameter is result, vector with K probabilities for the multinomial logistic regression model with predictors X. Estimate(Vector, Vector) Computes predicted probabilities for the multinomial logistic regression model with predictor X, X is M-by-P matrix with P predictor variables for each of M predictors. Second parameter is result, M-by-K matrix with K probabilities for each of M predictors. Estimate(Matrix, Matrix)	Single observation: Multiple observations:
Get β	The result β is a (P+1)-by-(K–1) matrix of estimate. Each column corresponds to the estimated intercept term and predictor coefficients, one for each of the first K–1 multinomial categories. The estimates for the K-th category are taken to be zero. GetFittedParameters
Estimate residuals	Computes deviance residuals for the observation. EstimateResidual(Vector, Vector) EstimateResiduals(Matrix, Matrix, Vector)

The class provides the following properties:

Property	Description
Status	Computation status: Can be on the following: MethodSucceeded indicates that model fitting was successful. MaximumIterations indicates that the maximum iterations number is exceeded before the algorithm converges.
Iterations	Amount of iterations to perform.
IterationsDone	Completed iterations.

The code demonstrates using of the MultinomialRegression class to build regression:

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.LeastSquares;
 4
 5namespace FinMath.Samples
 6{
 7    class MultinomialRegressionSample
 8    {
 9        static void Main()
10        {
11+Generate inputs.11-            #region Generate inputs.
12 
13             // Input Parameters.
14             const Int32 observations = 100;
15             const Int32 predictorsCount = 50;
16             const Int32 categoriesCount = 10;
17 
18             Random r = new Random((int)DateTime.Now.Ticks);
19 
20             Matrix regressors = Matrix.Random(observations, predictorsCount, r);
21             Matrix regressands = Matrix.Random(observations, categoriesCount, r);
22 
23             #endregion
24
25            // Build regression
26            MultinomialRegression regression = new MultinomialRegression(regressors, regressands);
27            // Get fitted parameters
28            Matrix fittedParameters = regression.GetFittedParameters();
29            //Compute estimates
30            Matrix Estimates = new Matrix(observations, categoriesCount);
31            regression.Estimate(regressors, Estimates);
32
33            Console.WriteLine("Parameters:");
34            Console.WriteLine("  Fitted parameters: ");
35            Console.WriteLine("  " + fittedParameters.ToString("0.000"));
36            Console.WriteLine("  Estimates: ");
37            Console.WriteLine("  " + Estimates.ToString("0.000"));
38            Console.ReadLine();
39        }
40    }
41}

Reference

Other Resources