Click or drag to resize

Weighted Least Squares (WLS)

This topic contains the following sections:

WLS is an extension of OLS to overcome one of the standard assumptions of the OLS, namely, the residuals homoscedasticity assumption.

In practice, it is quite common to observe situations where the variance of the noise depends on the value of the underlying variable, i.e. noise is heteroscedastic. The most common case is when the noise gets larger as the variable increases. In such a situation, the OLS is not the best linear prediction model anymore, and has to be replaced by the WLS.

WLS Specification

The general idea is that an observation with a large noise variance should be given less importance in defining the prediction than an observation with a small noise variance. More specifically, WLS estimator over n observations is found by:

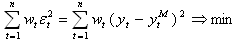
WLSProblem

where wt are the suitable weights to reduce the influence of residuals in regions of high noise variance.

The modified sum of squares yields the following normal equations:

X TW X b = X TW y

where:

  • X is the design matrix;

  • W is a diagonal matrix of weights;

  • y is the vector of regressand's observations;

  • b is the vector of unknown regression coefficients.

It is theoretically shown that the WLS is the best linear unbiased estimator if each weight is equal to the reciprocal of the variance of the measurement in the given observation:

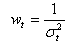
WLSWeights

In practice, these variances are usually unknown and should be somehow estimated. A frequently used approach is using of squared residuals produced by any (for instance OLS) model or expert as a first-step approximation.

Any algorithm for solving an OLS problem can be used to solve a weighted problem by scaling the observations and the design matrix.

WLS Implementation and Usage

WLS solver is implemented by the WeightedLS class.

To initialize a class instance use one of the two constructors provided:

  • WeightedLS(Int32) - allocates memory for a class instance with the specified number of regressors;

  • WeightedLS(Matrix, Vector, Vector) - creates a class instance and runs model fitting for the design matrix, regressand observations and user-specified weights associated with the observations; the results are available via methods and properties of basic interface.

The class extends the basic interface with the methods that can increase and decrease observation base, i.e. it is designed in such a way that it can recalculate regression by adding of new observations and 'forgetting' portions of previously used observations:

Operation

Description

Performance

LLS Bar 2

Increasing of observation base with new observations

Adding new observations to the model so that the resulting model coefficients are the same as they would computed with the whole (concatenated) set of weighted observations at once:

methodUpdate(Vector, Double, Double)

methodUpdate(Matrix, Vector, Vector)

Single observation:

Multiple observations:

Decreasing of observation base by excluding observations

Modifying the model by excluding some of the previously used weighted observations:

methodForget(Vector, Double, Double)

methodForget(Matrix, Vector, Vector)

Single observation:

Multiple observations:

Note Note

The class does not keep the weights applied when model building or recalculation.

The class provides the FitWLS(Matrix, Vector, Vector) static method to build weighted regression without initializing of class instance; this method is more resource consuming so not recommended for regularly repeated calculations.

Static are also convenience methods to compute the weights as reciprocals of the corresponding residuals' variances; all the variances less than the provided or default (Epsilon - the distance from 1.0 to the next double-precision number distinguishable from 1.0.) threshold value are replaced with the mean variance over the observations:

Code Sample

The sample demonstrates how to build a weighted regression using the OrdinaryLS class to compute the weights:

C#
Copy
 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.LeastSquares;
 4using FinMath.Statistics.Distributions;
 5
 6namespace FinMath.Samples
 7{
 8    class WeightedLSSample
 9    {
10        static void Main()
11        {
12-            #region Generate inputs.
13 
14             // Input Parameters.
15             const Int32 inSampleObservations = 100;
16             const Int32 outOfSampleObservations = 100;
17             const Int32 regresssorsCount = 10;
18             const Double maximumErrorVariance = 0.2;
19 
20             Uniform uniform = new Uniform(0.0, maximumErrorVariance);
21             // Here we generate synthetic data according to model: Y = X * Beta + Er. Er is heteroskedastic errors.
22             // Allocate real beta vector for model.
23             Vector realBeta = Vector.Random(regresssorsCount);
24             // Allocate in-sample error variance.
25             Vector inSampleVariances = Vector.Random(inSampleObservations, uniform);
26             // Allocate in-sample observation of regressors X.
27             Matrix inSampleRegressors = Matrix.Random(inSampleObservations, regresssorsCount);
28             // Allocate out-of-sample observation of regressors X.
29             Matrix outOfSamplesRegressors = Matrix.Random(outOfSampleObservations, regresssorsCount);
30 
31             // Calculate in-sample regressand values Y, without errors.
32             Vector inSampleRegressand = inSampleRegressors * realBeta;
33             // Calculate out-of-sample regressand values Y, without errors.
34             Vector outOfSamplesRegressand = outOfSamplesRegressors * realBeta;
35 
36             // Add noise. As far as our model is Y = X * Beta + Er. Where Er ~ N(0, v) and v is variance, different for each observation.
37             // Add errors to in-sample regressand values.
38             for (Int32 i = 0; i < inSampleObservations; ++i)
39                 inSampleRegressand[i] += Normal.Sample(0.0, inSampleVariances[i]);
40             // Add errors to out-of-sample regressand values. We do not store out-of-sample variances, so we generate it on the fly.
41             for (Int32 i = 0; i < inSampleObservations; ++i)
42                 outOfSamplesRegressand[i] += Normal.Sample(0.0, uniform.Sample());
43 
44             #endregion
45
46            // Find weights from known in-sample variances.
47            Vector weights = WeightedLS.VariancesToWeights(inSampleVariances);
48            // Compute least squares.
49            WeightedLS ls = new WeightedLS(inSampleRegressors, inSampleRegressand, weights);
50            // Get least squares beta.
51            Vector lsBeta = ls.Parameters;
52
53            Console.WriteLine("Parameters:");
54            Console.WriteLine("  Real parameters (which were used for data generation): ");
55            Console.WriteLine("  " + realBeta.ToString("0.000"));
56            Console.WriteLine("  Parameters calculated by least squares: ");
57            Console.WriteLine("  " + lsBeta.ToString("0.000"));
58
59            Console.WriteLine("");
60            Console.WriteLine("Least Squares Results:");
61            Console.WriteLine("  Parameters difference norm is: " + (realBeta - lsBeta).L2Norm());
62            // Build forecast for out-of-sample regressand values and estimate residuals.
63            Console.WriteLine("  Out-of-sample error is: " + ls.EstimateResiduals(outOfSamplesRegressors, outOfSamplesRegressand).L2Norm());
64        }
65    }
66}

It is also possible to organize updating of WLS model over a sliding data window like it is demonstrated in the Ordinary Least Squares (OLS) section.

See Also