Click or drag to resize

Generalized Least Squares (GLS)

This topic contains the following sections:

GLS is an extension of OLS which appeared to address the practical need to handle regression models with error terms that are heteroskedastic and/or correlated.

GLS Specification

The main idea of GLS is to find and apply some linear transformation to the standard regression model that scales and "de-correlates" residuals and, this way, meets the conditions of homoscedastic and uncorrelated residuals; in turn, these conditions make possible using OLS technique for the transformed model.

This idea was pioneered and theoretically grounded by A. Aitken. Aitken proved that the transformed regression model of the form:

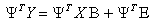
GLSTransform
produces the best linear unbiased estimator if the transformation matrix Ψ satisfies the equation:
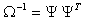
GLSCovariation
where Ω is the covariance matrix of the residuals.

The transformed problem takes the form:

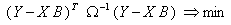
GLSProblem
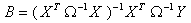
and the closed-form GLS estimator is written as:
GLSEstimator

The last equation shows how the GLS is related to OLS and WLS techniques:

  • if the covariance matrix Ω is diagonal with equal elements, then GLS is just OLS case (error terms are uncorrelated and homoskedastic);

  • If the covariance matrix is diagonal with non-constant diagonal elements, then the error terms are uncorrelated but heteroskedastic, and GLS reduces to WLS.

In practice correlated residuals are most commonly encountered with time-series data, and the correlations are usually highest for observations that are close in time. The main obstacle to use the GLS in practice is that the covariance matrix is unknown and one has to get some estimations of that matrix.

GLS Implementation and Usage

The GLS solver is implemented by the GeneralizedLS class.

Initialization of a class instance with the constructor GeneralizedLS(Matrix, Vector, Matrix) runs building of regression model for the input observations with user-specified covariance matrix.

Status and results of computation are available via basic methods and properties.

The FitGLS(Matrix, Vector, Matrix) static method provides building of regression model without initializing of an instance of the class.

Note Note

This method as well as other static methods are more resource consuming so not recommended for repeated calculations.

Code Sample

The example of GLS usage:

C#
Copy
 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.LeastSquares;
 4using FinMath.LinearAlgebra.Factorizations;
 5using FinMath.Statistics.Distributions;
 6using FinMath.Statistics;
 7
 8namespace FinMath.Samples
 9{
10    class GeneralizedLSSample
11    {
12        static void Main()
13        {
14-            #region Generate inputs.
15 
16             // Input Parameters.
17             const Int32 inSampleObservations = 100;
18             const Int32 outOfSampleObservations = 100;
19             const Int32 regresssorsCount = 10;
20             const Double maximumErrorVariance = 0.05;
21 
22             // Here we generate synthetic data according to model: Y = X * Beta + Er.
23             // Allocate real beta vector for model.
24             Vector realBeta = Vector.Random(regresssorsCount);
25             // Allocate in-sample observation of regressors X.
26             Matrix inSampleRegressors = Matrix.Random(inSampleObservations, regresssorsCount);
27             // Allocate out-of-sample observation of regressors X.
28             Matrix outOfSamplesRegressors = Matrix.Random(outOfSampleObservations, regresssorsCount);
29 
30             // Calculate in-sample regressand values Y, without errors.
31             Vector inSampleRegressand = inSampleRegressors * realBeta;
32             // Calculate out-of-sample regressand values Y, without errors.
33             Vector outOfSamplesRegressand = outOfSamplesRegressors * realBeta;
34 
35             // Create in-sample errors covariance matrix.
36             Matrix Q = new QR(Matrix.Random(inSampleObservations, inSampleObservations)).Q();
37             Matrix inSampleCcovarianceMatrix = Q * Matrix.Diagonal(inSampleObservations, FMControl.DefaultGenerator.Value.NextSeries(inSampleObservations, maximumErrorVariance / 10, maximumErrorVariance)) * Q.GetTransposed();
38             inSampleCcovarianceMatrix.EnsureRightBoundary(maximumErrorVariance);
39 
40             Matrix outOfSampleCcovarianceMatrix = Q * Matrix.Diagonal(outOfSampleObservations, FMControl.DefaultGenerator.Value.NextSeries(outOfSampleObservations, maximumErrorVariance / 10, maximumErrorVariance)) * Q.GetTransposed();
41             outOfSampleCcovarianceMatrix.EnsureRightBoundary(maximumErrorVariance);
42 
43             // Add noise. As far as our model is Y = X * Beta + Er. Where Er ~ N(0, Cov) and Cov is positive definite covariance matrix.
44             // Add errors to in-sample regressand values;
45             NormalMultivariate normalDistribution = new NormalMultivariate(new Vector(inSampleObservations, 0.0), inSampleCcovarianceMatrix);
46             inSampleRegressand.PointwiseAddInPlace(normalDistribution.Sample());
47             // Add errors to out-of-sample regressand values;
48             normalDistribution = new NormalMultivariate(new Vector(outOfSampleObservations, 0.0), outOfSampleCcovarianceMatrix);
49             outOfSamplesRegressand.PointwiseAddInPlace(normalDistribution.Sample());
50 
51             #endregion
52
53            // Compute least squares.
54            GeneralizedLS ls = new GeneralizedLS(inSampleRegressors, inSampleRegressand, inSampleCcovarianceMatrix);
55            // Get least squares beta.
56            Vector lsBeta = ls.Parameters;
57
58            Console.WriteLine("Parameters:");
59            Console.WriteLine("  Real parameters (which were used for data generation): ");
60            Console.WriteLine("  " + realBeta.ToString("0.000"));
61            Console.WriteLine("  Parameters calculated by least squares: ");
62            Console.WriteLine("  " + lsBeta.ToString("0.000"));
63
64            Console.WriteLine("");
65            Console.WriteLine("Least Squares Results:");
66            Console.WriteLine("  Parameters difference norm is: " + (realBeta - lsBeta).L2Norm());
67            // Build forecast for out-of-sample regressand values and estimate residuals.
68            Console.WriteLine("  Out-of-sample error is: " + ls.EstimateResiduals(outOfSamplesRegressors, outOfSamplesRegressand).L2Norm());
69        }
70    }
71}

See Also