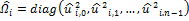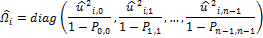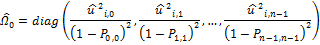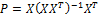Click or drag to resize

Feasible Weighted Least Squares (FWLS)

This topic contains the following sections:

The FWLS model operates with correlated and heteroscedastic residuals like the WLS does but the word Feasible underlines that the 'pure' WLS is commonly not feasible in practice as the covariance matrix of the residuals is unknown and effective estimation of the matrix is a separate, difficult and often impossible task.

The FWLS model suggests ways to overcome that difficulty under reasonable assumptions and to get the necessary estimations in process of model building.

FWLS Specification

FWLS algorithm assumes the diagonal estimation matrix, as the variances of the observed values are unequal (i.e. heteroscedasticity is present), but no correlations exist among the observed values.

FWLS is the iterative process. The following algorithm is applied:

  1. The ordinary least squares (OLS) estimator is calculated as usual by

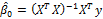
    FWLSBeta 0

    and estimates of the residuals are constructed:

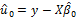
    FWLSResidual 0

  2. The covariance matrix is constructed according to one of the estimation methods:

  3. βi+1 is estimated using WLS:

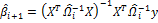
    FWLSBeta 1

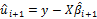
    FWLSResidual 1

  4. Returning to step 2 with residuals from the previous iteration until the specified number of iterations is reached.

FWLS Implementation and Usage

The FWLS solver is implemented by the FeasibleWLS class.

The implementation provides ability to select a suitable estimation of residuals’ covariance matrix; supported estimators are enumerated inside the class ( members of the FeasibleWLSVarianceVectorForm enumeration).

Each of the three constructors provided runs model building with either user-specific or default estimator (JackKnife) and number of iterations (2):

Status and results of computation are available via basic methods and properties.

The FitFeasibleWLS(Matrix, Vector, FeasibleWLSVarianceVectorForm, Int32) static method provides building of regression model without initializing of an instance of the class.

Note Note

As well as other static methods this method is more resource consuming so not recommended for repeated calculations.

Code Sample

The class does not require any additional efforts to compute covariances (if used):

C#
Copy
 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.LeastSquares;
 4using FinMath.Statistics.Distributions;
 5
 6namespace FinMath.Samples
 7{
 8    class FeasibleWLSSample
 9    {
10        static void Main()
11        {
12-            #region Generate inputs.
13 
14             // Input Parameters.
15             const Int32 inSampleObservations = 100;
16             const Int32 outOfSampleObservations = 100;
17             const Int32 regresssorsCount = 7;
18             const Double maximumErrorVariance = 0.3;
19 
20             Uniform uniform = new Uniform(0.0, maximumErrorVariance);
21 
22             // Here we generate synthetic data according to model: Y = X * Beta + Er. Er is heteroskedastic errors.
23             // Allocate real beta vector for model.
24             Vector realBeta = Vector.Random(regresssorsCount);
25             // Allocate in-sample observation of regressors X.
26             Matrix inSampleRegressors = Matrix.Random(inSampleObservations, regresssorsCount);
27             // Allocate out-of-sample observation of regressors X.
28             Matrix outOfSamplesRegressors = Matrix.Random(outOfSampleObservations, regresssorsCount);
29 
30             // Calculate in-sample regressand values Y, without errors.
31             Vector inSampleRegressand = inSampleRegressors * realBeta;
32             // Calculate out-of-sample regressand values Y, without errors.
33             Vector outOfSamplesRegressand = outOfSamplesRegressors * realBeta;
34 
35             // Add noise. As far as our model is Y = X * Beta + Er. Where Er ~ N(0, v) and v is variance, different for each observation.
36             // Add errors to in-sample regressand values. We do not store in-sample variances, so we generate it on the fly.
37             for (Int32 i = 0; i < inSampleObservations; ++i)
38                 inSampleRegressand[i] += Normal.Sample(0.0, uniform.Sample());
39             // Add errors to out-of-sample regressand values. We do not store out-of-sample variances, so we generate it on the fly.
40             for (Int32 i = 0; i < inSampleObservations; ++i)
41                 outOfSamplesRegressand[i] += Normal.Sample(0.0, uniform.Sample());
42 
43             Console.WriteLine("Real parameters (which were used for data generation): ");
44             Console.WriteLine("  " + realBeta.ToString("0.000"));
45 
46             #endregion
47
48            foreach (FeasibleWLS.VarianceVectorForm varianceEstimation in Enum.GetValues(typeof(FeasibleWLS.VarianceVectorForm)))
49            {
50                // Compute least squares. Number of steps is 2. Note: we assume in-sample variance is unknown.
51                FeasibleWLS ls = new FeasibleWLS(inSampleRegressors, inSampleRegressand, varianceEstimation, 2);
52
53                Console.WriteLine(varianceEstimation + ":");
54                // Get least squares beta.
55                Vector lsBeta = ls.Parameters;
56                Console.WriteLine("  Parameters: " + lsBeta.ToString("0.000"));
57                Console.WriteLine("  Parameters difference norm is: " + (realBeta - lsBeta).L2Norm());
58                // Build forecast for out-of-sample regressand values and estimate residuals.
59                Console.WriteLine("  Out-of-sample error is: " + ls.EstimateResiduals(outOfSamplesRegressors, outOfSamplesRegressand).L2Norm());
60            }
61        }
62    }
63}

See Also