Wilcoxon Rank Sum Test

Tail.Both must be set if in the alternative hypothesis the probability of a sample from the first distribution exceeding a sample from the second distribution (after exclusion of ties) is not equal to 0.5.

Tail.Left must be set if in the alternative hypothesis the probability of a sample from the first distribution exceeding a sample from the second distribution (after exclusion of ties) is lesser than 0.5.

Tail.Right must be set if in the alternative hypothesis the probability of a sample from the first distribution exceeding a sample from the second distribution (after exclusion of ties) is greater than 0.5.

The Wilcoxon rank sum test assumes the observations from both groups are independent of each other. The samples can have different lengths.

The following method is applied:

1. Both samples are sorted in non-decreasing order.

2. The ranks of the elements in the combined sample are obtained.

3. A method for handling ties is used. (A tie is counted when two observations are within fuzz of each other.) The average rank of the tied observations is calculated for handling tied observations between samples.

4. The rank sum function is computed as the sum of the ranks in the first sample.

5. Tie adjustment is computed using the following formula:

   

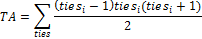
   where ties_i means the number of tied elements in tie i.

6. Mean and standard deviation are calculated:

   
   

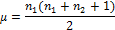
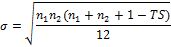
   where n₁ and n₂ are sizes of samples respectively and TS means tie score:

   

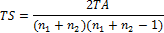
7. Test statistic is calculated as (rank sum - μ)/σ.

8. When one performs a Wilcoxon test for small samples, p-value is calculated exactly using the combinatorial method. For larger samples, a Normal distribution approximation is used and p-value is calculated approximately. Therefore, in general, decision based on p-value and significance level comparison is more exact.

The WilcoxonRankSumTest class inherits from the TwoSampleTest class. The following constructors create an instance of WilcoxonRankSumTest class.

The class provides the following methods:

The class provides the following properties:

The example of WilcoxonRankSumTest class usage:

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.Statistics.HypothesisTesting;
 4using FinMath.Statistics.Distributions;
 5
 6namespace FinMath.Samples
 7{
 8    class WilcoxonRankSumTestSample
 9    {
10        static void Main()
11        {
12            //Create instances of normal distribution.    
13            Normal distr1 = new Normal(0, 5);
14            Normal distr2 = new Normal(0.5, 5);
15
16            // Generate random series.
17            Vector series1 = Vector.Random(100, distr1);
18            Vector series2 = Vector.Random(150, distr2);
19
20            // Create an instance of WilcoxonRankSumTest.
21            WilcoxonRankSumTest test = new WilcoxonRankSumTest(0.05, Tail.Both);
22            test.Update(series1, series2);
23
24            Console.WriteLine("Test Result:");
25            // Test decision
26            Console.WriteLine($"  The null hypothesis failed to be rejected: {test.Decision}");
27            // The statistic of WilcoxonRankSumTest test.
28            Console.WriteLine($"  Statistics = {test.Statistics:0.000}");
29            // The p-value of the test statistic.
30            Console.WriteLine($"  P-Value = {test.PValue:0.000}");
31
32        }
33    }
34}

Reference