Chi Squared Variance Test

One-sample χ²-test of the null hypothesis that the data in the sample comes from a normal distribution with specified supposed variance, against the alternative that data comes from a normal distribution with a different variance.

This topic contains the following sections:

Chi Squared Variance Test Specification
Implementation
Code Sample
See Also

Chi Squared Variance Test Specification

This test can be either a two-sided test or a one-sided test. The two-sided version tests against the alternative that the true variance is either less than or greater than the specified value. The one-sided version only tests in one direction. The choice of a two-sided or one-sided test is determined by the problem. For example, if we are testing a new process, we may only be concerned if its variability is greater than the variability of the current process.

Consider s is a variance of a distribution, the chi-square hypothesis test is defined as:

H₀: s = s₀;

H_a:

s < s₀ for a left one-tailed test;
s < s₀ for a right one-tailed test;
s ≠ s₀ for a two-tailed test;

Test statistic is calculated as follows:

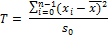
i.e. the sum of squares about the sample mean, divided by the nominal value for the variance (the value to be tested as holding).

Implementation

The following constructors create an instance of ChiSquaredVarianceTest class.

Constructor	Description	Performance
two-tailed test, default significance level	Constructor without parameters. Creates ChiSquaredVarianceTest instance with default significance level for two-tailed test. ChiSquaredVarianceTest
default significance level	Creates ChiSquaredVarianceTest instance with default significance level and user defined tail. ChiSquaredVarianceTest(Tail)
two-tailed test, user defined significance level	Creates ChiSquaredVarianceTest instance for two-tailed test and user-defined significance level. ChiSquaredVarianceTest(Double)
user defined tail and significance level	Creates ChiSquaredVarianceTest instance with user defined significance level and tail. ChiSquaredVarianceTest(Double, Tail)

The class provides the following methods:

Method	Description	Performance
update	Updates test statistic using provided sample and supposition about variance. Double array series: Update(Double, Double) Vector series: Update(Vector, Double)

Method

Description

Performance

update

Updates test statistic using provided sample and supposition about variance.

Double array series:

method Update(Double, Double)

Vector series:

method Update(Vector, Double)

The class provides the following properties:

Property	Description	Performance
region of acceptance	We fail to reject null hypothesis if test statistics is between left and right borders of region of acceptance. Region of acceptance left border: AcceptanceRegionLeft Region of acceptance right border: AcceptanceRegionRight
p-value	The probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. PValue

Property

Description

Performance

region of acceptance

We fail to reject null hypothesis if test statistics is between left and right borders of region of acceptance.

Region of acceptance left border:

Property AcceptanceRegionLeft

Region of acceptance right border:

Property AcceptanceRegionRight

p-value

The probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true.

Property PValue

Code Sample

The example of ChiSquaredVarianceTest class usage:

Copy

 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.Statistics.HypothesisTesting;
 4using FinMath.Statistics.Distributions;
 5
 6namespace FinMath.Samples
 7{
 8    class ChiSquaredVarianceTestSample
 9    {
10        static void Main()
11        {
12            //Create an instance of normal distribution.
13            Normal distr = new Normal(0, 1);
14
15            // Generate random series.
16            Vector series = Vector.Random(100, distr);
17
18            // Create an instance of ChiSquaredVarianceTest.
19            ChiSquaredVarianceTest test = new ChiSquaredVarianceTest(0.05, Tail.Both);
20            test.Update(series, 1);
21
22            Console.WriteLine("Test Result:");
23            // Test decision
24            Console.WriteLine($"  The null hypothesis failed to be rejected: {test.Decision}");
25            // The statistic of ChiSquaredVarianceTest test.
26            Console.WriteLine($"  Statistics = {test.Statistics:0.000}");
27            // The p-value of the test statistic.
28            Console.WriteLine($"  P-Value = {test.PValue:0.000}");
29
30        }
31    }
32}

Reference

FinMath.Statistics.HypothesisTesting