Click or drag to resize

Kwiatkowski-Phillips-Schmidt-Shin (KPSS) Test

This topic contains the following sections:

The KPSS Test has been developed to complement unit root tests as the last have low power with respect to near unit-root and long-run trend processes.

KPSS Test Specification

Unlike unit root tests, Kwiatkowski et al. provide straightforward test of the null hypothesis of trend stationarity against the alternative of a unit root.

For this, they consider three-component representation of the observed time series 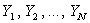ADF Time Series as the sum of a deterministic time trend, a random walk and a stationary residual:

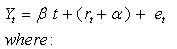
KPSS Model

  • rt = rt-1 + ut is a random walk, the initial value r0 = α serves as an intercept,

  • t is the time index,

  • ut are independent identically distributed KPSS UDistribution.

The simplified version of the model without the time trend component is also used to test level stationarity.

The null and the alternative hypotheses are formulated as follows:

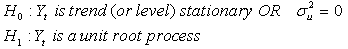
KPSS Hypotheses

KPSS Test Implementation and Usage

The KPSSTest class implements KPSS Test procedure according to the specification above. This class inherits from the OneSampleTest class.

The following constructors create an instance of KPSSTest class.

Constructor

Description

Performance

set significanceLevel, numberOfLags, and includeTrend

Initializes an instance of KPSSTest for the input parameters specified:

significanceLevel is the desired significance level of the test in the range 0.01 – 0.1,

numberOfLags is the non-negative integer indicating the number of autocovariance lags to include in the Newey-West estimator of the long-run variance,

includeTrend boolean value indicating whether or not to include the deterministic trend term in the model.

methodKPSSTest(Double, Int32, Boolean)

The following public properties provide the details about the model and decision made:

Property

Description

Performance

decision

The result of testing: takes true if the stationarity null hypothesis is accepted while the false value means rejecting of the null hypothesis in favor of the alternative unit root hypothesis.

PropertyDecision

statistic

Shows the value of KPSS statistic.

PropertyStatistic

p-value

The probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true.

PropertyPValue

c-value

Shows the critical value of the KPSS statistic at the input significance level.

PropertyCValue

sse

The sum of squared errors.

PropertySSE

alpha

The intercept constant or drift (the α in the specification).

PropertyAlpha

beta

The coefficient β on a time trend.

PropertyBeta

region of acceptance

We fail to reject null hypothesis if test statistics is between left and right borders of region of acceptance.

Region of acceptance left border:

PropertyAcceptanceRegionLeft

Region of acceptance right border:

PropertyAcceptanceRegionRight

Note Note

There is also the indicator-style implementation of the KPSS Test available in the Financial Analysis library and referred to as

C#
Copy
1QuantOffice.FinancialAnalysis.TA.Kpss
That implementation is more adopted to handle time series data either in expanding or sliding window manner. See the corresponding documentation for details.

Code Sample

The example of KPSSTest class usage:

C#
Copy
 1using System;
 2using FinMath.LinearAlgebra;
 3using FinMath.Statistics.HypothesisTesting;
 4
 5namespace FinMath.Samples
 6{
 7    class KPSSTestSample
 8    {
 9        static void Main()
10        {
11            // Generate random series.
12            Vector series = Vector.Random(100);
13
14            // Create an instance of ADFTest.
15            KPSSTest test = new KPSSTest(0.05, 2, true);
16            test.Update(series);
17
18            Console.WriteLine("Test Result:");
19            // Test's decision.
20            Console.WriteLine($"  Stationary? = {!test.Decision}");
21            // The statistic of KPSS test.
22            Console.WriteLine($"  Statistics = {test.Statistic:0.000}");
23            // The c-value of the test statistic.
24            Console.WriteLine($"  C-Value = {test.CValue:0.000}");
25            // The p-value of the test statistic.
26            Console.WriteLine($"  P-Value = {test.PValue:0.000}");
27
28            Console.WriteLine("Model Details:");
29            // The intercept constant or drift.
30            Console.WriteLine($"  Alpha = {test.Alpha:0.000}");
31            // The coefficient on a time trend.
32            Console.WriteLine($"  Beta = {test.Beta:0.000}");
33
34            Console.WriteLine("Extra Information:");
35            // The sum of squared errors.
36            Console.WriteLine($"  SSE = {test.SSE:0.000}");
37        }
38    }
39}

See Also